题目内容
8. 如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.
如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.
分析 先根据图形旋转的性质得出CE的长,再根据直角三角形的性质得出∠CED的度数,进而得出∠BCE的度数,由扇形的面积公式即可得出结论.
解答 解:∵线段CE由线段BC旋转而成,BC=4,
∴CE=BC=4.
∵AB=2,∠ABD=90°,
∴∠CED=30°.
∵AD∥BC,
∴∠BCE=∠CED=30°,
∴S阴影=$\frac{30π×{4}^{2}}{360}=\frac{4π}{3}$.
故答案为:$\frac{4π}{3}$
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )| A. | $\frac{π+\sqrt{2}-1}{2}$cm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{4π+3\sqrt{3}-3}{6}$cm2 | D. | $\frac{π+\sqrt{3}-1}{2}$cm2 |
20.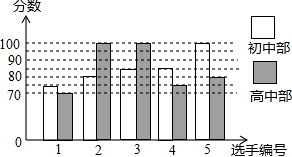 某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
求得初中代表队选手决赛成绩的平均数和方差:
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85,
${{S}_{1}}^{2}$=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70;
(1)根据图示填写表格:
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
 某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.求得初中代表队选手决赛成绩的平均数和方差:
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85,
${{S}_{1}}^{2}$=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70;
(1)根据图示填写表格:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
(3)计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
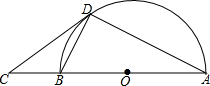 如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.
如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.