题目内容
3.解方程组:(1)$\left\{\begin{array}{l}{x+y=2}\\{x-y=4}\end{array}\right.$
(2)$\left\{\begin{array}{l}{y=2x-1}\\{3x-y=3}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用代入消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+y=2①}\\{x-y=4②}\end{array}\right.$,
①+②得:2x=6,即x=3,
把x=3代入①得:y=-1,
则方程组的解$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{y=2x-1①}\\{3x-y=3②}\end{array}\right.$,
把①代入②得:3x-2x+1=3,即x=2,
把x=2代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.下面计算中,正确的是( )
| A. | (-2mn)3=8m3n3 | B. | (m+n)3(m+n)2=m5+n5 | C. | -(a3b2)3=-a9b6 | D. | (-$\frac{1}{3}$a4b)2=$\frac{1}{6}$a6b2 |
15.在学校乒乓球比赛中,从陈亮、李明、刘松、周杰、王刚这五人中,随机抽签一组对手,正好抽到王刚与刘松的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{4}$ |
12.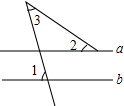 如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )
如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )
 如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )
如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )| A. | 75° | B. | 50° | C. | 35° | D. | 30° |
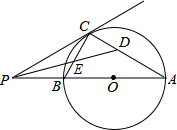 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.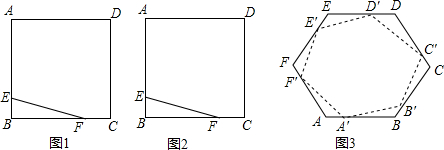
 如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.
如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.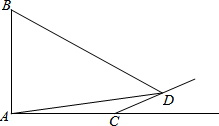 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位).
如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位).