题目内容
18.(1)$(\sqrt{24}-\sqrt{\frac{1}{2}})-(\sqrt{\frac{1}{8}}+\sqrt{6})$(2)计算:$(2\sqrt{3}+\sqrt{6})(2\sqrt{3}-\sqrt{6})$
(3)化简:$\sqrt{3}$($\sqrt{8}$+$\sqrt{3}$)-($\sqrt{54}$+6)÷$\sqrt{6}$.
分析 (1)原式去括号合并即可得到结果;
(2)原式利用平方差公式计算即可得到结果;
(3)原式利用二次根式的乘除法则计算即可得到结果.
解答 解:(1)原式=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$=$\sqrt{6}$-$\frac{3\sqrt{2}}{4}$;
(2)原式=12-6=6;
(3)原式=2$\sqrt{6}$+3-3-$\sqrt{6}$=$\sqrt{6}$.
点评 此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.下面计算中,正确的是( )
| A. | (-2mn)3=8m3n3 | B. | (m+n)3(m+n)2=m5+n5 | C. | -(a3b2)3=-a9b6 | D. | (-$\frac{1}{3}$a4b)2=$\frac{1}{6}$a6b2 |
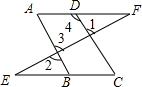 如图,已知∠1=∠2,∠A=∠C,证明:AF∥EC.
如图,已知∠1=∠2,∠A=∠C,证明:AF∥EC.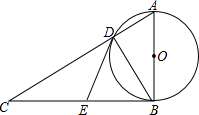 如图,在⊙O中,AB为直径,BC为⊙O的切线,D为⊙O上一点,AD的延长线与切线BC交于点C,E是BC的中点,连接DE,BD.
如图,在⊙O中,AB为直径,BC为⊙O的切线,D为⊙O上一点,AD的延长线与切线BC交于点C,E是BC的中点,连接DE,BD. 如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.
如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.