题目内容
4．在△ABC中，AB=AC=5，点D为BC边上一点，且AD=4，BD=3，则DC=3．分析 根据题意画出图形，利用勾股定理的逆定理判断出△ABD是直角三角形，再由等腰三角形的性质即可得出结论．
解答 
解：如图，在△ABD中，
∵AB=5，AD=4，BD=3，
∴AB2=AD2+BD2，
∴△ABD是直角三角形，
∴AD⊥BC．
∵AB=AC，
∴DC=BD=3．
故答案为：3．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，平面直角坐标系中，AB=CD，OA=OC，且OB=3，则D点坐标是（-3，0）．
如图，△ABC中，AB=AC，∠B=∠C=40°，点E、F在BC边上，∠AEF=70°，∠AFE=60°，求线段BE、EF、CF围成的三角形的各内角度数．
19．小夏是一位善于观察、勤于动脑的学生．一天，他从2017年某个月日历表中随机框取了相邻的四个数（如图所示），分别用a，b，c，d表示．略加思考后，他写出了三个关系式：①a+c=b+d；②c-a=b-d；③ac-bd=7．其中正确的有（ ）
| 2017年 月 农历丙申（猴）年辛丑月 建国68年 | ||||||
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 初五 | 2 初六 | 3 立夏初七 | 4 初八 | |||
| a | d | |||||
| b | c | |||||
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
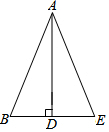已知：如图，△ABE中，AD平分∠BAE，且AD⊥BE，垂足为D．
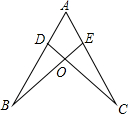如图，点D，E分别在线段AB，AC上，CD与BE相交于O点、已知AB=AC，BD=CE，求证：∠B=∠C．