Question

13．已知△ABC中，AB=AC=5，cosB=$\frac{3}{5}$，将△ABC绕点C旋转，得到△A₁B₁C．
（1）如图1，若点B₁在线段BA的延长线上
①求证：AB∥A₁C；
②求△AB₁C的面积；
（2）如图2，点D为线段AC中点，点E是线段AB上的动点，在△ABC绕点C旋转过程中，点E的对应点是点E₁，求线段DE₁长度的最大值和最小值．

Answer 1

分析 （1）①根据旋转的性质和平行线的性质证明；
②过A作AF⊥BC于F，过C作CM⊥AB于M，根据三角函数和三角形的面积公式解答；
（2）过C作CE⊥AB于E，以C为圆心CE为半径画圆交AC于E₁，得出最小值解答即可．

解答 解：（1）①证明：∵AB=AC，
∴∠B=∠ACB，
∵B₁C=BC
∴∠1=∠B，
∵∠2=∠ACB（旋转角相等），
∴∠1=∠2，
∴AB∥A₁C；
②过A作AF⊥BC于F，过C作CM⊥AB于M，如图1，

∵AB=AC，AF⊥BC
∴BF=CF
∵$cosB=\frac{3}{5}$，AB=5，
∴BF=3
∴BC=6
∴B₁C=BC=6，
∵CM⊥AB
∴BM=B₁M=$\frac{18}{5}$
∴BB₁=$\frac{36}{5}$，CM=$\frac{24}{5}$，
∴AB₁=$\frac{36}{5}-5=\frac{11}{5}$，
∴△AB₁C的面积为：$\frac{1}{2}×\frac{11}{5}×\frac{24}{5}=\frac{132}{25}$；
（2）如图2过C作CE⊥AB于E，以C为圆心CE为半径画圆交AC于E₁，DE₁有最小值．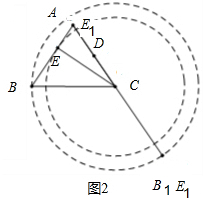

此时在Rt△BEC中，CE=$\frac{24}{5}$，
∴CE₁=$\frac{24}{5}$，
∴DE₁的最小值为CE₁-CD=$\frac{24}{5}-\frac{5}{2}=\frac{23}{10}$；
如图，以C为圆心BC为半径画圆交AC的延长线于E₁，
DE₁有最大值．
此时DE₁=DC+BC=$\frac{5}{2}$+6=$\frac{17}{2}$．

点评 此题考查几何变换问题，关键是根据旋转的性质和三角形的面积公式进行解答．