题目内容
5.我市干鲜经销公司,进了一种海味虾米共2000千克.进价为每千克20元,物价局规定其销售单价不得高于每千克50元,也不得低于每千克20元.市场调查发现:单价定为50元时,每天平均销售30千克;单价每降低1元,每天平均多售出2千克.在销售过程中,每天还要支出其他费用400元(天数不足一天时按整天计算).设销售单价为每千克x元,每天平均获利为y元,请解答下列问题:(1)求y关于x的函数关系式,并写出x的取值范围.
(2)当销售单价是每千克多少元时,每天平均获利最多,最多利润是多少元?
(3)若将这种虾米全部售出,比较每天平均获利最多和销售单价最高这两种销售方式,哪一种获总利润最多?多多少?
分析 (1)由日均获利y=(售价-成本)×销售量-其他费用400元,由此关系式列出函数关系式;
(2)由(1)中的关系式配方,求最大值.
(3)分别计算出日均获利最多时的利润额和销售单价最高时的利润额,做差比较即可.
解答 解:(1)y=(x-20)(30+2•$\frac{50-x}{1}$)-400=-2x2+170x-3000 (20≤x≤50),
答:y与x之间的函数关系式为y=-2x2+170x-3000(20≤x≤50);
(2)y=-2x2+170x-3000=-2(x-$\frac{85}{2}$)2+612.5
∵a=-2<0,
∴二次函数开口向下,
∴当x=$\frac{85}{2}$时,y最大=612.5
答:当销售单价是每千克$\frac{85}{2}$元时,每天平均获利最多,最多利润是612.5元;
(3)当每日平均获利最多时,x=$\frac{85}{2}$,日销售量=30+2×(50-x)=45,
∴销售天数为2000÷45=44$\frac{4}{9}$≈45,
∴获总利润为:($\frac{85}{2}$-20)×2000-45×400=27000(元);
当销售单价最高时,x=50,日销售量=30,
∴销售天数为2000÷30=66$\frac{2}{3}$≈67
∴获总利润为:2000×(50-20)-67×400=33200;
故当销售单价最高时获总利润最多.
33200-27000=6200(元)
答:销售单价最高这种销售方式获总利润最多,多6200元.
点评 本题考查了二次函数的实际应用,依据:销售问题的数量关系日获利=每千克的获利×销售数量-支出费用运用,求出函数的解析式是关键.

练习册系列答案
相关题目
13.下列格式,运算正确的是( )
| A. | a6÷a2=a3 | B. | (-3a2)2=9a4 | C. | 3a+4b=7ab | D. | 2a-2=$\frac{1}{2{a}^{2}}$ |
10.不等式组$\left\{\begin{array}{l}{-2x+1<x+4}\\{\frac{x}{2}-\frac{x-1}{3}≤1}\end{array}\right.$的整数解( )个.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.某种衬衫的价格经过连续两次的降价后,由每件150元降到96元,则平均每次降价的百分率是( )
| A. | 10% | B. | 15% | C. | 20% | D. | 30% |

 在某大型娱乐场,景点A、B、C依次位于同一直线上(如图),B处是登高观光电梯的入口.已知A、C之间的距离为70米,EB⊥AC,电梯匀速运行10秒可从B处到达D处,此时可观察到景点C,电梯再次以相同的速度匀速运行30秒可到达E处,此时可观察到景点A.在D、E处分别测得∠BDC=60°,∠BEA=30°,求电梯在上升过程中的运行速度.
在某大型娱乐场,景点A、B、C依次位于同一直线上(如图),B处是登高观光电梯的入口.已知A、C之间的距离为70米,EB⊥AC,电梯匀速运行10秒可从B处到达D处,此时可观察到景点C,电梯再次以相同的速度匀速运行30秒可到达E处,此时可观察到景点A.在D、E处分别测得∠BDC=60°,∠BEA=30°,求电梯在上升过程中的运行速度. 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )



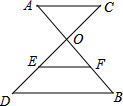 如图,AB、CD相交于点O,OC=2,OD=3,AC∥BD,EF是△ODB的中位线,且EF=2,则AC的长为$\frac{8}{3}$.
如图,AB、CD相交于点O,OC=2,OD=3,AC∥BD,EF是△ODB的中位线,且EF=2,则AC的长为$\frac{8}{3}$.