题目内容
15.如图1,在平面直角坐标系xOy中,点B(-2,2),过反比例函数y=$\frac{k}{x}$(x<0,常数k<0)图象上一点A(-$\frac{1}{2}$,m)作y轴的平行线交直线l:y=x+2于点C,且AC=AB.
(1)分别求出m、k的值,并写出这个反比例函数解析式;
(2)发现:过函数y=$\frac{k}{x}$(x<0)图象上任意一点P,作y轴的平行线交直线l于点D,请直接写出你发现的PB,PD的数量关系PB=PD;
应用:①如图2,连接BD,当△PBD是等边三角形时,求此时点P的坐标;
②如图3,分别过点P、D作y的垂线交y轴于点E、F,问是否存在点P,使得矩形PEFD的周长取得最小值?若存在,请求出此时点P的坐标及矩形PEFD的周长;若不存在,请说明理由.
分析 (1)求出AC、AB的表达式,根据AC=AB求出m的值,然后利用待定系数法求出k的值即可;
(2)设P(-m,$\frac{2}{m}$)(m>0),则D(-m,-m+2),根据勾股定理求出PB的长即可;①由△PBD是等边三角形,于是得到PB=BD=PD,根据等边三角形的性质得到(2-m)=$\frac{1}{2}$$\sqrt{3}$($\frac{2}{m}$+m-2)解得:m=3-$\sqrt{3}$,或m=$\sqrt{3}$-1,于是得到P($\sqrt{3}$-3,$\frac{3-\sqrt{3}}{3}$)或P(1-$\sqrt{3}$,$\sqrt{3}$+1);②根据矩形的周长的计算公式得到矩形PEFD的周长=($\frac{2}{\sqrt{m}}$-$\sqrt{m}$)2+4,根据二次函数的性质即可得到结论.
解答 解:(1)AC=m-$\frac{3}{2}$,AB=$\sqrt{\frac{9}{4}+(m-2)^{2}}$,
∵AC=AB,
∴m=4,
∴点A(-$\frac{1}{2}$4),
∴k=-2,
∴y=-$\frac{2}{x}$(x<0);
(2)设P(-m,$\frac{2}{m}$)(m>0),则D(-m,-m+2),
∴PD=$\frac{2}{m}$-(-m+2)=$\frac{2}{m}$+m-2,
BP=$\sqrt{(m+2)^{2}+(-\frac{2}{m}-2)^{2}}$=$\sqrt{(\frac{2}{m}+m-2)^{2}}$=$\frac{2}{m}$+m-2,
∴PD=PB;
故答案为:PB=PD;
①∵△PBD是等边三角形,
∴PB=BD=PD,
∵PD∥y轴,
∴(2-m)=$\frac{1}{2}$$\sqrt{3}$($\frac{2}{m}$+m-2)
∴$\frac{2}{m}$+m-2=$\sqrt{(m+2)^{2}+(m+2-2)^{2}}$,
∴m=3-$\sqrt{3}$,或m=$\sqrt{3}$-1,
∴P(1-$\sqrt{3}$,$\sqrt{3}$+1);
②答:存在满足题设条件的点P.
设P(-m,$\frac{2}{m}$)(m>0),则D(-m,-m+2),
∴矩形PEFD的周长=2(PD+PE)=2($\frac{2}{m}$+m-2+m)=$\frac{4}{m}$+4m-4=($\frac{2}{\sqrt{m}}$-$\sqrt{m}$)2+3m,
∴当$\frac{2}{\sqrt{m}}$-$\sqrt{m}$=0,即m=2时,P(-1,2)时,矩形PEFD的周长取得最小值为4.
点评 本题考查了反比例函数综合题,涉及勾股定理、存在性问题,综合性很强,要灵活处理,同时注意从多角度解题.

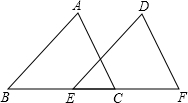 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )| A. | ∠A=∠D | B. | BC=EF | C. | ∠ACB=∠F | D. | AC=DF |
| 每天的定价x(元/间) | 208 | 228 | 268 | … |
| 每天的房间空闲数y(间) | 10 | 15 | 25 | … |
(2)如果宾馆每天的日常运营成本为5000元,另外,对有顾客居住的房间,宾馆每天每间还需支出28元的各种费用,那么单纯从利润角度考虑,宾馆应将房间定价确定为多少时,才能获得最大利润?并请求出每天的最大利润.
| 老师在课堂上放手让学生提问和表达情况调查 | |||||
| 选项 | A | B | C | D | E |
| 内容 | 从不 | 很少 | 有时 | 常常 | 总是 |
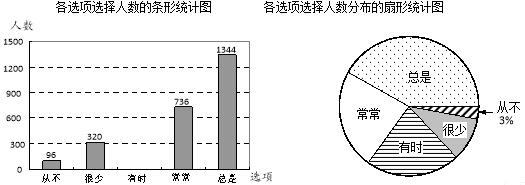
根据以上信息,解答下列问题:
(1)该区参加了本次问卷调查的八年级的学生共有多少名?
(2)请把这幅条形统计图补充完整.
(3)在扇形统计图中,“总是”所占的百分比多少?
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
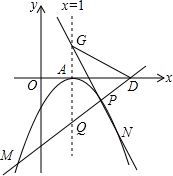 如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.
如图,已知直线y=kx+b(k>0)交抛物线y=-(x-1)2交于M、P两点,交抛物线对称轴x=1于Q(Q在x轴下方),交x轴于D,点N是点M关于对称轴x=1的对称点,延长NP交对称轴x=1于G,求证:DG=DQ.