题目内容
17. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是( )| A. |  | B. |  | C. |  | D. |  |
分析 可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.
解答 解:根据勾股定理,AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,BC=$\sqrt{2}$,
所以,夹直角的两边的比为$\frac{2\sqrt{2}}{\sqrt{2}}$=2,
观各选项,只有B选项三角形符合,与所给图形的三角形相似.
故选:B.
点评 此题考查了勾股定理在直角三角形中的运用,三角形对应边比值相等判定三角形相似的方法,本题中根据勾股定理计算三角形的三边长是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
12.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过15分钟的频率是( )
| 通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 16 | 9 | 5 |
| A. | 0.1 | B. | 0.4 | C. | 0.5 | D. | 0.9 |
2. 如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
 如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-$\frac{3}{x}$的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
6.据统计结果显示,我市今年约有120000名学生参加中考,120000这个科学记数法可表示为( )
| A. | 12×104 | B. | 1.2×105 | C. | 1.2×104 | D. | 0.12×106 |
7.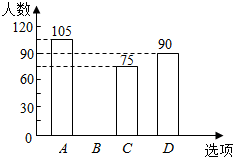 某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
请结合统计图表,回答下列问题:
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.
 某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 朗诵 | 25% |
| D | 器乐 | 30% |
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.


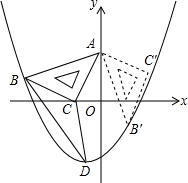 如图,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.
如图,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.