题目内容
6.在△ABC中,AB=AC.(1)如图①,若P是BC上的任意一点,连接AP,求证:AB2-AP2=BP•CP;
(2)如图②,若P是BC延长线上的一点,连接AP,则还能得到(1)中的结论吗?请说明理由.
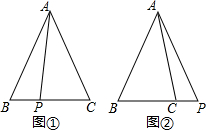
分析 (1)过A作AM⊥BC于M,AB2=AM2+BM2,AP2=AM2+MP2,利用平方差公式,结合图形,即可得出结论;
(2)过A作AM⊥BC于M,AB2=AM2+BM2,AP2=AM2+MP2,利用平方差公式,结合图形,即可得出结论;
解答  (1)证明:如图①所示:过A作AM⊥BC于M,
(1)证明:如图①所示:过A作AM⊥BC于M,
则在Rt△ABM和Rt△APM中,
AB2=AM2+BM2,AP2=AM2+MP2,
则AB2-AP2=BM2-MP2=(BM+MP)(BM-MP)=CP(CM-MP)=BP•CP;
(2)解:不能成立;理由如下:如图②所示:
过A作AM⊥BC于M,
则在Rt△ABM和Rt△APM中,
AB2=AM2+BM2,AP2=AM2+MP2
AP2-AB2=MP2-BM2=(MP+BM)(MP-BM)=BP(MP-CM)=BP•CP,
∴AP2-AB2=BP•CP.
点评 本题考查了勾股定理的知识,解答本题的关键是熟练掌握勾股定理及平方差公式的形式.

练习册系列答案
相关题目
14.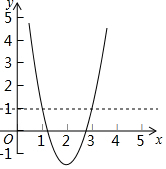 如图,二次函数y=ax2+bx+c(a>0)的图象与直线y=1交点坐标为(1,1),(3,1),则不等式ax2+bx+c-1>0的解集为( )
如图,二次函数y=ax2+bx+c(a>0)的图象与直线y=1交点坐标为(1,1),(3,1),则不等式ax2+bx+c-1>0的解集为( )
 如图,二次函数y=ax2+bx+c(a>0)的图象与直线y=1交点坐标为(1,1),(3,1),则不等式ax2+bx+c-1>0的解集为( )
如图,二次函数y=ax2+bx+c(a>0)的图象与直线y=1交点坐标为(1,1),(3,1),则不等式ax2+bx+c-1>0的解集为( )| A. | x>1 | B. | 1<x<3 | C. | x<1或x>3 | D. | x>3 |
15.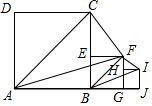 如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )
如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )
 如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )
如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )| A. | 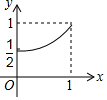 | B. | 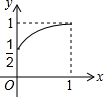 | C. | 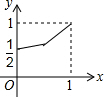 | D. | 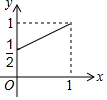 |
15.有一块长为m,宽为n的长方形铝片,四角各截去一个相同的边长为x的小正方形,折起来做成一个没有盖的盒子,则此盒子的体积可表示为( )
| A. | x(m-x)(n-x) | B. | x2(m-x)(n-x) | C. | $\frac{1}{3}$x(m-2n)(n-2x) | D. | x(m-2x)(n-2x) |
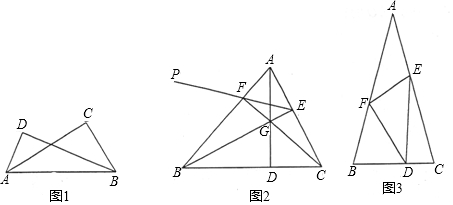
 如图,BD和EC相交于点A,ED∥BC,BD=12,AD=4,EC=9,则AC=?
如图,BD和EC相交于点A,ED∥BC,BD=12,AD=4,EC=9,则AC=?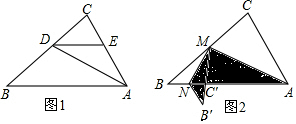
 如图,以AB为直径的⊙O中,CD是弦,CD∥AB,连接AC,BD交于点M.
如图,以AB为直径的⊙O中,CD是弦,CD∥AB,连接AC,BD交于点M.