题目内容
11.△ABC中,AB=6,AC=4,BC=5.(1)如图1,若AD是∠BAC的平分线,DE∥AB,求CE的长与$\frac{CD}{BD}$的比值;
(2)如图2,将边AC折叠,使得AC在AB边上,折痕为AM,再将边MB折叠,使得MB'与MC'重合,折痕为MN,求AN的长.
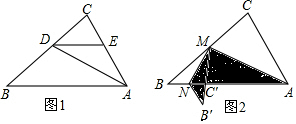
分析 (1)先判定三角形ADE是等腰三角形,再根据平行线分线段成比例定理,求得CE的长;
(2)先根据两角对应相等,判定△ABC∽△NB′C′,再根据相似三角形的对应边成比例,求得NC′与B′N的数量关系,最后结合BC′的长为2,求得NC′的长,进而得到AN的长度.
解答 解:(1)∵AD是∠BAC的平分线,DE∥AB,
∴∠EAD=∠BAD=∠EDA,
∴ED=EA,即△ADE是等腰三角形,
设CE=x,则AE=4-x=DE,
∵DE∥AB,
∴$\frac{DE}{BA}$=$\frac{CE}{CA}$,即$\frac{4-x}{6}$=$\frac{x}{4}$,
解得,CE=1.6,
∵DE∥AB,
∴$\frac{CD}{BD}$=$\frac{CE}{EA}$=$\frac{2}{3}$;
(2))由折叠得,∠B=∠B′,∠C=∠MC′A=∠B′C′N,AC=AC′=4,
∴△ABC∽△NB′C′,
∴$\frac{NC′}{NB′}$=$\frac{AC}{AB}$=$\frac{2}{3}$,
设NC′=2a,则BN=B′N=3a,
∵BC=AB-AC′=6-4=2,
∴NC′+BN=2,即2a+3a=2,
解得a=0.4,
∴NC′=2a=4.8,
∴AN=NC′+N′A=4.8.
点评 本题考查了平行线分线段成比例定理以及相似三角形的判定与性质,具有一定的难度.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,解题时应重点把握对应边相等,对应角相等.

练习册系列答案
相关题目
2.我国古代典籍《庄子•天下篇》中曾说过一句话:“一尺之棰,日取其半,万世不竭”,现有一根长为1尺的木杆,第1次截取其长度的一半,第2次截取其第1次剩下长度的一半,第3次截取其第2次剩下长度的一半,如此反复,则第99次截取后,此木杆剩下的长度为( )
| A. | $\frac{1}{2^{98}}$尺 | B. | $\frac{1}{2^{99}}$尺 | C. | $\frac{1}{2^{100}}$尺 | D. | $\frac{1}{{2}^{101}}$尺 |
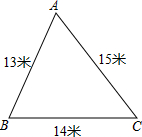 学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?
 如图,AB长为2$\sqrt{3}$,BC长为4,AF长为10,求正方形CDEF的周长.
如图,AB长为2$\sqrt{3}$,BC长为4,AF长为10,求正方形CDEF的周长.