题目内容
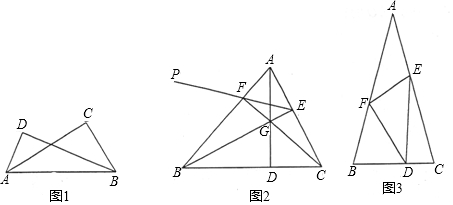
16.(1)如图l,Rt△ABD和Rt△ABC的斜边为AB,直角顶点D、C在AB的同侧,求证:A、B、C、D四个点在同一个圆上.(2)如图2,△ABC为锐角三角形,AD⊥BC于点D,CF⊥AB于点F,AD与CF交于点G,连结BG并延长交AC于点E,作点D关于AB的对称点P,连结PF.求证:点P、F、E三点在一条直线上.
(3)如图3,△ABC中,∠A=30°,AB=AC=2,点D、E、F分别为BC、CA、AB边上任意一点,△DEF的周长有最小值,请你直接写出这个最小值.
分析 (1)取AB的中点O,连结OD,OC,根据OA=OB=OC=OD,可得A、B、C、D四个点在同一个圆上;
(2)连结DF,根据∠1=∠2,且AD⊥BC于点D,CF⊥AB于点F,得出点B、F、E、C四点共圆,∠3=∠4,再根据∠2+∠BFE=180°,得出∠1+∠BFE=180°,即可得到点P、F、E三点在一条直线上;
(3)作点D关于AB的对称点G,作点D关于AC的对称点H,连接GF,HE,则DF=GF,DE=HE,当点G,F,E,H在同一直线上时,GF+FE+EH=GH(最短),此时,DF+FE+DE最短,即△DEF的周长有最小值,连接BE,先求得BE=$\frac{1}{2}$AB=1,再根据勾股定理在Rt△BCE中,求得BC的长,最后根据面积法得出$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×AC×BE,即可得到AD 的长.
解答 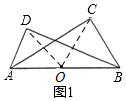 解:(1)如图1,取AB的中点O,连结OD,OC,
解:(1)如图1,取AB的中点O,连结OD,OC,
∵Rt△ABD和Rt△ABC的斜边为AB,
∴OD=$\frac{1}{2}AB$,OC=$\frac{1}{2}AB$,
∴OA=OB=OC=OD,
∴A、B、C、D四个点在同一个圆上.
(2)如图2,连结DF,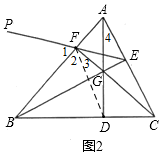
∵点D、P关于AB对称,
∴∠1=∠2,
∵AD⊥BC于点D,CF⊥AB于点F,
∴∠2+∠3=90°,∠4+∠BCE=90°,BE⊥AC,点A、C、D、F四点共圆,
∴点B、F、E、C四点共圆,∠3=∠4,
∴∠2=∠BCE,∠BFE+∠BCE=180°,
∴∠2+∠BFE=180°,
∴∠1+∠BFE=180°,
∴点P、F、E三点在一条直线上.
(3)如图3,作点D关于AB的对称点G,作点D关于AC的对称点H,连接GF,HE,则DF=GF,DE=HE,
∴当点G,F,E,H在同一直线上时,GF+FE+EH=GH(最短),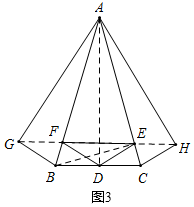
此时,DF+FE+DE最短,即△DEF的周长有最小值,
由轴对称的性质,可得∠GAH=2∠BAC=60°,AG=AD=AH,
∴△AGH是等边三角形,
∴△DEF的周长最小值=GH=AD,
∵当AD⊥BC时,AD有最小值,
∴当AD⊥BC时,△DEF的周长有最小值,
连接BE,
由∠CEH=∠ECH=75°可得,EH=CH,
又∵DE=EH,BD=DC=CH,
∴DE=DC=DB,
∴∠BEC=90°,
∴Rt△ABE中,BE=$\frac{1}{2}$AB=1,AE=$\sqrt{3}$,
∴EC=2-$\sqrt{3}$,
∴Rt△BCE中,BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=2$\sqrt{2-\sqrt{3}}$=2×$\frac{\sqrt{6}-\sqrt{2}}{2}$=$\sqrt{6}$-$\sqrt{2}$,
∵$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×AC×BE,
∴$\frac{1}{2}$×($\sqrt{6}$-$\sqrt{2}$)×AD=$\frac{1}{2}$×2×1,
∴AD=$\frac{2}{\sqrt{6}-\sqrt{2}}$=$\frac{{\sqrt{6}+\sqrt{2}}}{2}$,
即△DEF的周长有最小值$\frac{{\sqrt{6}+\sqrt{2}}}{2}$.
点评 本题属于三角形综合题,主要考查了四点共圆,直角三角形的性质,等腰三角形的性质,轴对称的性质以及勾股定理的综合应用,解决问题的关键是作辅助线,根据两点之间线段最短进行计算求解.解题时注意:面积法的运用可以容易求得等腰三角形底边上的高.如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.

 优学名师名题系列答案
优学名师名题系列答案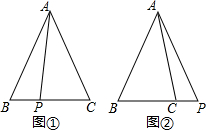
 如图,梯形ABCD中,BD平分∠ABC,AD⊥BD.若AD=4,DC=6,则tanA=2$\sqrt{2}$.
如图,梯形ABCD中,BD平分∠ABC,AD⊥BD.若AD=4,DC=6,则tanA=2$\sqrt{2}$.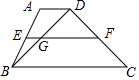 如图,梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点G,若AD=2,EF=5,那么FG=4.
如图,梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点G,若AD=2,EF=5,那么FG=4.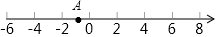 如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.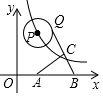 如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.
如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.