题目内容
10.抛物线y=ax2+bx+c(a≠0)的顶点为D(1,4),交x轴于A、B两点,且经过点C(2,3)(1)求抛物线的解析式;
(2)如图,M为线段O、B之间一动点,N为y轴正半轴上一动点,是否存在使M、C、D、N四点围成的四边形周长最小?若存在,求出这个最小值及M、N的坐标;若不存在,请说明理由;
(3)若P是y轴上的点,Q是抛物线上的点,求:以P、Q、A、B为顶点构成平行四边形的点Q的坐标.
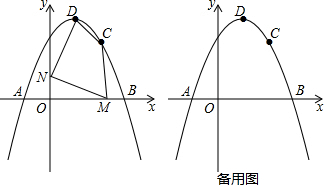
分析 (1)设抛物线的表达式为:y=a(x-1)2+4,将C(2,3)代入即可求出a.
(2)如图1中,作D(1,4)关于y轴对称点G(-1,4),C(2,3)关于x轴对称点H(2,-3),连接GH与x轴交于点M,与y轴交于点N,此时四边形CDNM周长最小.利用两点距离公式求出GH,CD即可解决周长的最小值,再求出直线GH即可解决点M、N坐标.
(3)分AB为边、AB为对角线两种情形解决即可.AB为边时注意也有两种情形①当点Q在轴的右侧时,②当点Q在y轴的左侧时;若AB为平行四边形的对角线,如图2,过Q作QF⊥x轴,垂足为F,利用△POB≌△QFA解决问题.
解答 解:(1)设抛物线的表达式为:y=a(x-1)2+4,
将C(2,3)代入,解得:a=-1
∴抛物线的表达式为:y=-x2+2x+3.
(2)作D(1,4)关于y轴对称点G(-1,4),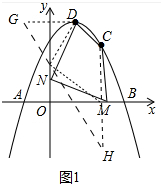
C(2,3)关于x轴对称点H(2,-3),
∵CD是一个定值,∴要使四边形MCDN的周长最小,
只要使DN+MN+MC最小即可
由图形的对称性,可知,
DN+MN+MC=GN+NM+HM,
只有当GH为一条直线段时,
可求得:CD=$\sqrt{2}$,GH=$\sqrt{58}$,
∴四边形MCDN的周长最小为$\sqrt{2}$+$\sqrt{58}$,
此时直线GH为y=-$\frac{7}{3}$x+$\frac{5}{3}$,
∴点N(0,$\frac{5}{3}$),点M(0,$\frac{5}{7}$).
(3)若AB为平行四边形的边,∵AB=4,AB∥PQ且AB=PQ,以为顶点的四边形构成平行四边形,
①当点Q在轴的右侧时,xQ=4,又∵点Q在抛物线上,
∴yQ=-5,∴Q1(4,-5),
②当点Q在y轴的左侧时,xQ=-4,又∵点Q在抛物线上,
∴yQ=-21,∴Q2(-4,-21),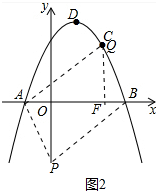
若AB为平行四边形的对角线,如图2,过Q作QF⊥x轴,垂足为F,
∵四边形PAQB为平行四边形,
∴AQ=PB,AQ∥PB,
∴∠QAF=∠PBO
在△AFQ和△BOP中,
$\left\{\begin{array}{l}{∠QAF=∠PBO}\\{∠AFQ=∠POB=90°}\\{AQ=PB}\end{array}\right.$,
∴△POB≌△QFA,
∴AF=OB=1
∴xQ=2,又∵点Q在抛物线上,∴yQ=3,∴Q3(2,3),
综上:符合要求的点Q的坐标为:Q1(4,-5),Q2(-4,-21),Q3(2,3).
点评 本题考查二次函数、一次函数、平行四边形的性质、对称等知识,学会待定系数法确定函数解析式,利用对称求最小值问题,第三个问题学会分类讨论,利用全等三角形的性质是解题的关键,属于中考压轴题.

 某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.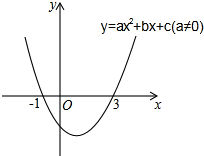 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当-1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是( ) 解不等式组$\left\{\begin{array}{l}{x+3≥4①}\\{3x-4≤11②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{x+3≥4①}\\{3x-4≤11②}\end{array}\right.$ 如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.
如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.