题目内容
6.计算:(1)(2$\sqrt{3}$+$\sqrt{2}$)(2$\sqrt{3}$-$\sqrt{2}$);
(2)$\frac{2}{\sqrt{3}+1}$+$\frac{\sqrt{3}}{2}$+1;
(3)$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$);
(4)3$\sqrt{8}$+2$\sqrt{18}$-3$\sqrt{22}$-$\sqrt{72}$;
(5)($\frac{3}{4}\sqrt{15}$-$\sqrt{12}$)$÷\frac{\sqrt{3}}{2}$.
分析 (1)原式利用平方差公式计算即可得到结果;
(2)原式分母有理化,合并即可得到结果;
(3)原式各项化简后,合并即可得到结果;
(4)原式各项化简后,合并即可得到结果;
(5)原式利用多项式除以单项式法则计算即可得到结果.
解答 解:(1)原式=12-2=10;
(2)原式=$\sqrt{3}$-1+$\frac{\sqrt{3}}{2}$+1=$\frac{3\sqrt{3}}{2}$;
(3)原式=3$\sqrt{2}$-$\sqrt{2}$-2$\sqrt{2}$=0;
(4)原式=6$\sqrt{2}$+6$\sqrt{2}$-3$\sqrt{22}$-6$\sqrt{2}$=6$\sqrt{2}$-3$\sqrt{22}$;
(5)原式=$\frac{3\sqrt{5}}{2}$-4.
点评 此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
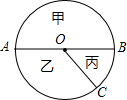 如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1
如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1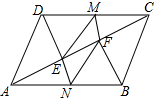 已知:?ABCD中,DE⊥AC于E,BF⊥AC于F,M,N分别是DC,AB的中点.求证:四边形MENF是平行四边形.
已知:?ABCD中,DE⊥AC于E,BF⊥AC于F,M,N分别是DC,AB的中点.求证:四边形MENF是平行四边形.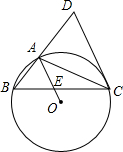 已知,如图,在△ABC中,∠B=45°,∠BCA=30°,过点A、B、C三点作⊙O,过点C作⊙O的切线交BA延长线于点D,连接OA交BC于E.
已知,如图,在△ABC中,∠B=45°,∠BCA=30°,过点A、B、C三点作⊙O,过点C作⊙O的切线交BA延长线于点D,连接OA交BC于E.