题目内容
17.一次函数y=-x+5与y=2x-1的图象交点在直线y=kx-7上,则k的值为5.分析 联立y=-x+5与y=2x-1,组成方程组,解方程组可得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,进而可得两函数交点为(2,3),再把(2,3)代入y=kx-7可得k的值.
解答 解:$\left\{\begin{array}{l}{y=-x+5}\\{y=2x-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
则一次函数y=-x+5与y=2x-1的图象交点为(2,3),
∵交点(2,3)在直线y=kx-7上,
∴3=2k-7,
解得:k=5,
故答案为:5.
点评 此题主要考查了一次函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点,必能满足解析式.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
7.已知一个多边形的最小的外角是60°,其余外角依次增加20°,则这个多边形的边数为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
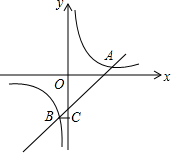 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$和直线y=kx+b交于A,B两点,A(5,1),BC⊥y轴于C,且OC=5BC.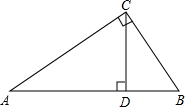 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高.
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高. 如图,△ABC的周长为24,AC的垂直平分线交BC于点D,垂足为E,若AE=4,则△ADB的周长是16.
如图,△ABC的周长为24,AC的垂直平分线交BC于点D,垂足为E,若AE=4,则△ADB的周长是16.