题目内容
7.已知一个多边形的最小的外角是60°,其余外角依次增加20°,则这个多边形的边数为( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据多边形的外角和等于360°确定边数的范围,分情况讨论即可.
解答 解:∵多边形的外角和等于360°,多边形的最小的外角是60°,
∴这个多边形的边数<$\frac{360}{60}$=6,
当边数为3时,60°+80°+100°<360°,不合题意,
当边数为4时,60°+80°+100°+120°=360°,符合题意,
当边数为5时,60°+80°+100°+120°+140°>360°,不合题意.
故选:C.
点评 本题考查的是多边形的内角与外角,掌握多边形的外角和等于360°是解题的关键,注意分情况讨论思想的运用.

练习册系列答案
相关题目
17.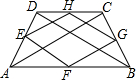 如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )
如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )
 如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )
如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )| A. | S1>2S2 | B. | 2S1<S2 | C. | S1=2S2 | D. | $\sqrt{{S}_{1}}$=2$\sqrt{{S}_{2}}$ |
15.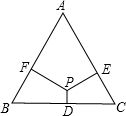 如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
 如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )| A. | 10 | B. | 15 | C. | $\frac{40}{3}$ | D. | $\frac{50}{3}$ |
16.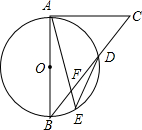 如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
 如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
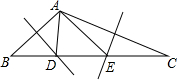 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E. 已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标.
已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标.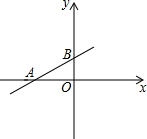 如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2).
如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2).