题目内容
6.如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含端点),过点P作PF⊥BC于点F,点D,E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.(1)求抛物线的解析式;
(2)若d=|PD-PF|.请说明d是否为定值?若是定值,请求出其大小;若不是定值,请说明其变化规律?
(3)求出△PDE周长取值范围.

分析 (1)利用待定系数法求出抛物线解析式即可;
(2)首先表示出P,F点坐标,再利用两点之间距离公式得出PD,PF的长,进而求出即可;
(3)过E作EF⊥x轴,交抛物线于点P,求得C△PDE=ED+PE+PD=ED+PE+PF+2=ED+2+(PE+PF),当P、E、F三点共线时,PE+PF最小;当P与A重合时,PE+PF最大;即可解答.
解答 解:(1)∵边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,
∴C(0,8),A(-8,0),
设抛物线解析式为:y=ax2+c,
则$\left\{\begin{array}{l}{c=8}\\{64a+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{8}}\\{c=8}\end{array}\right.$
∴抛物线解析式为$y=-\frac{1}{8}{x^2}+8$.
(2)设P(x,-$\frac{1}{8}$x2+8),则F(x,8),
则PF=8-(-$\frac{1}{8}$x2+8)=$\frac{1}{8}$x2.
PD2=x2+[6-(-$\frac{1}{8}$x2+8)]2=$\frac{1}{64}{x^4}+\frac{1}{2}{x^2}+4={(\frac{1}{8}{x^2}+2)^2}$
∴PD=$\frac{1}{8}{x^2}+2$,
∴d=|PD-PF|=$|{\frac{1}{8}{x^2}+2-\frac{1}{8}{x^2}}|$=2
∴d=|PD-PF|为定值2;
(3)如图,过点E作EF⊥x轴,交抛物线于点P,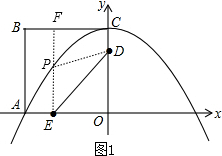
由d=|PD-PF|为定值2,
得C△PDE=ED+PE+PD=ED+PE+PF+2=ED+2+(PE+PF),
又∵D(0,6),E(-4,0)
∴$DE=\sqrt{{6^2}+{4^2}}=\sqrt{52}=2\sqrt{13}$
∴${C_{△PDE}}=2\sqrt{13}+2+(PE+PF)$,
当PE和PF在同一直线时PE+PF最小,
得C△PDE最小值$2\sqrt{13}+2+8=2\sqrt{13}+10$.
设P为抛物线AC上异于点A的任意一点,过P作PM∥x轴,交AB于点M,连接ME,如图2.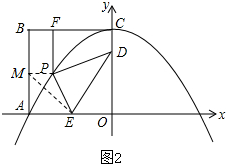
由于E是AO的中点,易证得ME≥PE(当点P接近点A时,在△PME中,显然∠MPE是钝角,故ME≥PE,与A重合时,等号成立),而ME≤AE+AM,
所以PE≤AE+AM.
所以当P与A重合时,PE+PF最大,
AE=8-4=4,PD=$\sqrt{A{O}^{2}+D{O}^{2}}=\sqrt{{8}^{2}+{6}^{2}}$=10.
得C△PDE最大值=2$\sqrt{13}$+4+10=$2\sqrt{13}+14$.
∴$2\sqrt{13}+10≤{C_{△PDE}}≤2\sqrt{13}+14$.
点评 此题主要考查了二次函数综合以及两点距离公式以及配方法求二次函数最值等知识,利用数形结合得出符合题意的答案是解题关键.

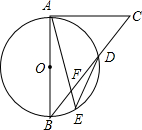 如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )
如图,AB为⊙O的直径,CA为⊙O的切线,CB交⊙O于D,$\widehat{AD}$=$\widehat{DE}$,AE交BD于F,若DF=BF,则tan∠BDE的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
| A. | k=-1 | B. | k=1 | C. | k=±1 | D. | k≠0 |
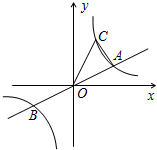 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=$\frac{k}{x}$上一点,且点C在直线y=$\frac{1}{2}$x的上方.
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=$\frac{k}{x}$上一点,且点C在直线y=$\frac{1}{2}$x的上方.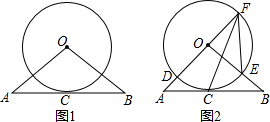
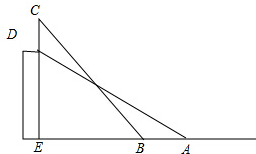 如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号).
如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号).