题目内容
5．抛物线y=ax2-2x与x轴正半轴相交于点A，顶点为B．（1）用含a的式子表示点B的坐标；
（2）经过点C（0，-2）的直线AC与OB（O为原点）相交于点D，与抛物线的对称轴相交于点E，△OCD≌△BED，求a的值．
分析 （1）利用配方法即可求得B的坐标；
（2）依据△OCD≌△BED可得BE=CO，据此即可求得BF的长，根据B的坐标求得a的值．
解答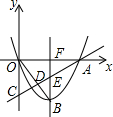 
解：（1）y=ax2-2x=a（x-$\frac{1}{a}$）2-$\frac{1}{a}$，则B的坐标是（$\frac{1}{a}$，-$\frac{1}{a}$）；
（2）∵点C的坐标是（0，-2），
∴OC=2，
设抛物线的对称轴与x轴相交于点F．
∵EF∥y轴，F是OA的中点，
∴EF=$\frac{1}{2}$CO=1．
∵△OCD≌△BED，
∴BE=CO=2，
∴BF=BE+EF=3．
∴-$\frac{1}{a}$=-3，
∴a=$\frac{1}{3}$．
点评 本题考查了二次函数的顶点坐标的确定以及全等三角形的性质，求得BF的长是关键．
练习册系列答案
相关题目
15．
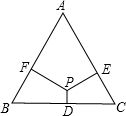如图，P为等腰三角形ABC内一点，过P分别作三条边BC、CA、AB的垂线，垂足分别为D、E、F．已知AB=AC=10，BC=12，且PD：PE：PF=1：3：3．则四边形PDCE的面积为（ ）
如图，P为等腰三角形ABC内一点，过P分别作三条边BC、CA、AB的垂线，垂足分别为D、E、F．已知AB=AC=10，BC=12，且PD：PE：PF=1：3：3．则四边形PDCE的面积为（ ）| A． | 10 | B． | 15 | C． | $\frac{40}{3}$ | D． | $\frac{50}{3}$ |
16．
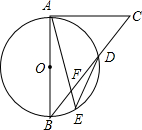如图，AB为⊙O的直径，CA为⊙O的切线，CB交⊙O于D，$\widehat{AD}$=$\widehat{DE}$，AE交BD于F，若DF=BF，则tan∠BDE的值为（ ）
如图，AB为⊙O的直径，CA为⊙O的切线，CB交⊙O于D，$\widehat{AD}$=$\widehat{DE}$，AE交BD于F，若DF=BF，则tan∠BDE的值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
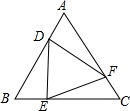如图，等边△ABC中，点D、E、F分别同时从点A、B、C出发，以相同的速度在AB、BC、CA上运动，连结DE、EF、DF．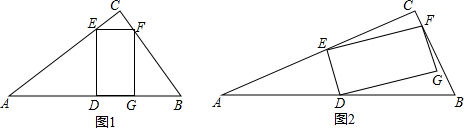
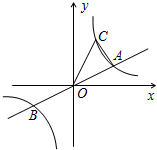10．（-$\frac{1}{3}$）-1-4cos30°+|-$\sqrt{12}$|的计算结果为（ ）
| A． | -4 | B． | 4 | C． | -3 | D． | -2 |
如图，已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A、B两点，点B的坐标为（-4，-2），C为第一象限内双曲线y=$\frac{k}{x}$上一点，且点C在直线y=$\frac{1}{2}$x的上方．