题目内容
20. 如图,正比例函数y=-2x与反比例函数$y=\frac{k}{x}$的图象在第二象限交于点A(-1,m),将函数y=-2x的图象向下平移3个单位长度与反比例函数$y=\frac{k}{x}$的图象分别交于B、C两点,连结AB,AC.
如图,正比例函数y=-2x与反比例函数$y=\frac{k}{x}$的图象在第二象限交于点A(-1,m),将函数y=-2x的图象向下平移3个单位长度与反比例函数$y=\frac{k}{x}$的图象分别交于B、C两点,连结AB,AC.(1)求反比例函数的解析式;
(2)求△ABC的面积.
分析 (1)根据点A(-1,m)在函数y=-2x的图象上,可得点A(-1,2),代入反比例函数$y=\frac{k}{x}$,可得k的值;
(2)通过解方程组可得点B(-2,1),C($\frac{1}{2}$,-4),过点A作AD∥y轴交直线BC于点D(-1,-1),根据割补法即可得到△ABC的面积.
解答 解:(1)∵点A(-1,m)在函数y=-2x的图象上,
∴m=-2×(-1)=2,
∴点A(-1,2),
代入反比例函数$y=\frac{k}{x}$,可得k=-1×2=-2,
∴反比例函数的解析式为$y=-\frac{2}{x}$;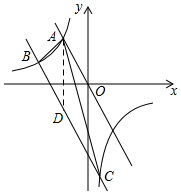
(2)由题意知,直线BC为y=-2x-3,
由$\left\{\begin{array}{l}y=-2x-3\\ y=-\frac{2}{x}\end{array}\right.$得$\left\{\begin{array}{l}{x_1}=-2\\{y_1}=1\end{array}\right.$,$\left\{\begin{array}{l}{x_2}=\frac{1}{2}\\{y_2}=-4\end{array}\right.$,
∴点B(-2,1),C($\frac{1}{2}$,-4),
如图,过点A作AD∥y轴交直线BC于点D,
在y=-2x-3中,令x=-1,则y=-1,
即D(-1,-1),
∴${S_{△ABC}}={S_{△ABD}}+{S_{△ADC}}=\frac{1}{2}•AD•({x_C}-{x_B})$
$\begin{array}{l}=\frac{1}{2}•AD•({x_C}-{x_B})=\frac{1}{2}•(2+1)•(\frac{1}{2}+2)\\=\frac{15}{4}\end{array}$
故△ABC的面积为$\frac{15}{4}$.
点评 本题考查了反比例函数与一次函数的交点问题以及待定系数法求函数解析式,解题时注意:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,反比例函数与一次函数图象的交点坐标满足两函数解析式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
| 等级 | 一分钟跳 绳次数x | 人数 |
| A | x>180 | 12 |
| B | 150<x≤180 | 14 |
| C | 120<x≤150 | a |
| D | x≤120 | b |
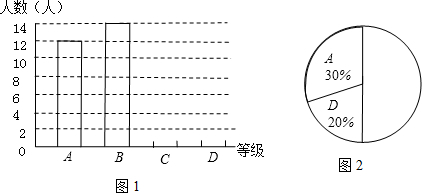
请结合图表完成下列问题:
(1)表1中a=6,b=8;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为200人.
 ”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )
”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )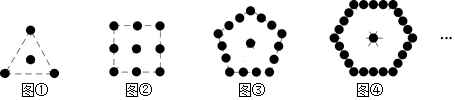
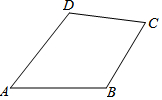 如图,在四边形ABCD中,AB=AD,CB=CD.请你添加一条线把它分成两个全等三角形,并给出证明.
如图,在四边形ABCD中,AB=AD,CB=CD.请你添加一条线把它分成两个全等三角形,并给出证明.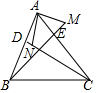 如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.
如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.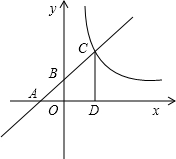 如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.