题目内容
10. 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
分析 先利用等腰直角三角形的性质得∠A=∠ACB=45°,再利用邻补角的定义计算出∠BCB′=135°,然后根据旋转的性质确定旋转角的大小.
解答 解:∵△ABC为等腰直角三角形,
∴∠A=∠ACB=45°,
∴∠BCB′=180°-45°=135°,
∵等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,
∴∠BCB′等于旋转角,
即旋转角为135°.
故选D.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
2.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元;
(1)当1≤x<50时,求出y与x的函数关系式;
(2)问销售该商品第几天时,销售利润最大,最大利润是多少?
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 70 |
| 每天销量(件) | 200-2x | |
(1)当1≤x<50时,求出y与x的函数关系式;
(2)问销售该商品第几天时,销售利润最大,最大利润是多少?
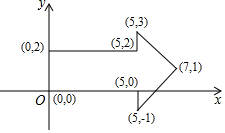 如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换:
如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换:
 如图,在△ABC中,∠ABC=45°,高AD,BE交于H点,若CD=5,则DH=5.
如图,在△ABC中,∠ABC=45°,高AD,BE交于H点,若CD=5,则DH=5. 如图,矩形ABCD的对角线经过原点,各边分别平行于坐标轴,点C在反比例函数y=$\frac{{k}^{2}-5k}{x}$的图象上.若点A的坐标为(-2,-3),则k的值为-1或6.
如图,矩形ABCD的对角线经过原点,各边分别平行于坐标轴,点C在反比例函数y=$\frac{{k}^{2}-5k}{x}$的图象上.若点A的坐标为(-2,-3),则k的值为-1或6. 如图,已知△ABC,用尺规作出BC边上的高AD(保留作图痕迹,不写作法).
如图,已知△ABC,用尺规作出BC边上的高AD(保留作图痕迹,不写作法). 如图,正比例函数y=-2x与反比例函数$y=\frac{k}{x}$的图象在第二象限交于点A(-1,m),将函数y=-2x的图象向下平移3个单位长度与反比例函数$y=\frac{k}{x}$的图象分别交于B、C两点,连结AB,AC.
如图,正比例函数y=-2x与反比例函数$y=\frac{k}{x}$的图象在第二象限交于点A(-1,m),将函数y=-2x的图象向下平移3个单位长度与反比例函数$y=\frac{k}{x}$的图象分别交于B、C两点,连结AB,AC.