题目内容
10.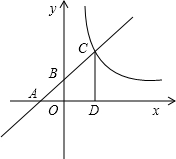 如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.(1)一次函数和反比例函数的解析式;
(2)求△ACD的面积.
分析 (1)根据OA=OB=OD=1和各坐标轴上的点的特点易得到点A、B、D的坐标,将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,由C点在一次函数的图象上可确定C点坐标,再将C点坐标代入y=$\frac{m}{x}$可确定反比例函数的解析式.
(2)根据A(-1,0),C(1,2),D(1,0),即可得到AD=2,CD=2,进而得出△ACD的面积.
解答 解:(1)∵OA=OB=OD=1,
∴点A、B、D的坐标分别为A(-1,0),B(0,1),D(1,0),
∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}{-k+b=0}\\{b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为y=x+1.
把x=1代入y=x+1得,y=2,
即点C的坐标是(1,2),
又∵点C在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,
∴m=2,
∴反比例函数的解析式为y=$\frac{2}{x}$.
(2)∵CD垂直于x轴,A(-1,0),C(1,2),D(1,0),
∴AD=2,CD=2,
∴△ACD的面积为$\frac{1}{2}$CD×AD=$\frac{1}{2}$×2×2=2.
点评 本题主要考查了一次函数与反比例函数交点问题,解决问题的关键是利用待定系数法求出函数解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.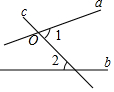 如图,直线a,b被直线c所截,记a与c的交点为O,且∠1=65°,∠2=45°,若要使a∥b,则a需绕点O( )
如图,直线a,b被直线c所截,记a与c的交点为O,且∠1=65°,∠2=45°,若要使a∥b,则a需绕点O( )
 如图,直线a,b被直线c所截,记a与c的交点为O,且∠1=65°,∠2=45°,若要使a∥b,则a需绕点O( )
如图,直线a,b被直线c所截,记a与c的交点为O,且∠1=65°,∠2=45°,若要使a∥b,则a需绕点O( )| A. | 逆时针旋转25° | B. | 逆时针旋转20° | C. | 顺时针旋转25° | D. | 顺时针旋转20° |
 如图,正比例函数y=-2x与反比例函数$y=\frac{k}{x}$的图象在第二象限交于点A(-1,m),将函数y=-2x的图象向下平移3个单位长度与反比例函数$y=\frac{k}{x}$的图象分别交于B、C两点,连结AB,AC.
如图,正比例函数y=-2x与反比例函数$y=\frac{k}{x}$的图象在第二象限交于点A(-1,m),将函数y=-2x的图象向下平移3个单位长度与反比例函数$y=\frac{k}{x}$的图象分别交于B、C两点,连结AB,AC. 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732)
如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732) 如图,已知△ABC.
如图,已知△ABC. 小新将一个有污渍的正方体纸盒沿如图所示的粗实线剪开,并展成平面图,其展开图为( )
小新将一个有污渍的正方体纸盒沿如图所示的粗实线剪开,并展成平面图,其展开图为( )


