题目内容
15.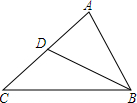 如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )
如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )| A. | ∠C=∠ABD | B. | ∠ABC=∠ADB | C. | $\frac{BD}{BC}$=$\frac{AD}{AC}$ | D. | $\frac{BD}{BC}$=$\frac{AD}{AB}$ |
分析 由AB是AD与AC的比例中项,得到$\frac{AB}{AC}=\frac{AD}{AB}$,由于∠A=∠A,推出△ABD∽△ACB,于是得到结论.
解答 解:∵AB是AD与AC的比例中项,
∴$\frac{AB}{AC}=\frac{AD}{AB}$,
∵∠A=∠A,
∴△ABD∽△ACB,
∴∠C=∠ABD,故A正确;
∠ABC=∠ADB,故B正确;
$\frac{BD}{BC}=\frac{AD}{AB}$,故C错误,D正确.
故选C.
点评 本题考查了相似三角形的判定和性质,找准对应顶点是解题的关键.

练习册系列答案
相关题目
20. 矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在线段BC上,F在线段BC上,且BF:FC=1:2,AF分别与DE,DB交于点M,N,则MN=( )
矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在线段BC上,F在线段BC上,且BF:FC=1:2,AF分别与DE,DB交于点M,N,则MN=( )
 矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在线段BC上,F在线段BC上,且BF:FC=1:2,AF分别与DE,DB交于点M,N,则MN=( )
矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在线段BC上,F在线段BC上,且BF:FC=1:2,AF分别与DE,DB交于点M,N,则MN=( )| A. | $\frac{3\sqrt{5}}{7}$ | B. | $\frac{5\sqrt{5}}{14}$ | C. | $\frac{9\sqrt{5}}{28}$ | D. | $\frac{11\sqrt{5}}{28}$ |
 设有理数a,b在数轴上的对应点如图所示,化简|a+b|-|a|-|1-b|+|-b|.
设有理数a,b在数轴上的对应点如图所示,化简|a+b|-|a|-|1-b|+|-b|.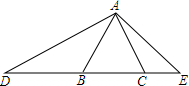 如图,在△ABC中,AB=AC,D、E为直线BC上的两点,且满足AB2=DB•CE,若∠BAC=50°,则∠DAE的度数为115°.
如图,在△ABC中,AB=AC,D、E为直线BC上的两点,且满足AB2=DB•CE,若∠BAC=50°,则∠DAE的度数为115°.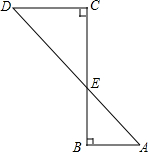 如图,∠A=θ,∠B=∠C=90°,AD与BC相交于点E,已知AD=m,AB=n,则CD等于mcosθ-n.
如图,∠A=θ,∠B=∠C=90°,AD与BC相交于点E,已知AD=m,AB=n,则CD等于mcosθ-n.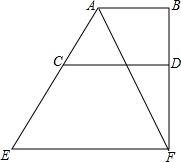 如图,AB⊥BF,CD⊥BF.∠BAF=∠AFE,求证:∠DCE+∠E=180°.
如图,AB⊥BF,CD⊥BF.∠BAF=∠AFE,求证:∠DCE+∠E=180°.