题目内容
4.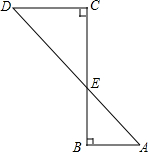 如图,∠A=θ,∠B=∠C=90°,AD与BC相交于点E,已知AD=m,AB=n,则CD等于mcosθ-n.
如图,∠A=θ,∠B=∠C=90°,AD与BC相交于点E,已知AD=m,AB=n,则CD等于mcosθ-n.
分析 先证明△CDE∽△BAE,得出对应边成比例$\frac{CD}{BA}=\frac{DE}{AE}$,再由三角函数求出AE,得出DE,即可求出CD.
解答 解:∵∠B=∠C=90°,∠DEC=∠AEB,
∴△CDE∽△BAE,
∴$\frac{CD}{BA}=\frac{DE}{AE}$,
∴CD=$\frac{DE}{AE}×BA$,
∵cosA=$\frac{AB}{AE}$,
∴AE=$\frac{AB}{cosA}$=$\frac{n}{cosθ}$,
∴DE=AD-AE=m-$\frac{n}{cosθ}$,
∴CD=$\frac{m-\frac{n}{cosθ}}{\frac{n}{cosθ}}$×n=mcosθ-n;
故答案为:mcosθ-n.
点评 本题考查了相似三角形的判定与性质、三角函数;熟练掌握相似三角形的判定与性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.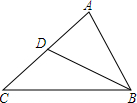 如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )
如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )
 如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )
如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )| A. | ∠C=∠ABD | B. | ∠ABC=∠ADB | C. | $\frac{BD}{BC}$=$\frac{AD}{AC}$ | D. | $\frac{BD}{BC}$=$\frac{AD}{AB}$ |
 如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y 平方米,AB长为x米.
如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y 平方米,AB长为x米.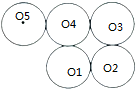 有5个半径相等的圆,排成如图所示图形,点O5是最左上方这个圆的圆心,现在要过点O5作一条直线将5个圆分成面积相等的两部分,请你根据所学知识试一试.
有5个半径相等的圆,排成如图所示图形,点O5是最左上方这个圆的圆心,现在要过点O5作一条直线将5个圆分成面积相等的两部分,请你根据所学知识试一试.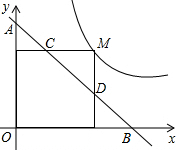 如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-$\sqrt{3}$x+m于点D、C两点,若直线y=-$\sqrt{3}$x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为4.
如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-$\sqrt{3}$x+m于点D、C两点,若直线y=-$\sqrt{3}$x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为4. 如图,四边形DEFG是△ABC的内接正方形,AB=BC=6cm,∠B=45°,则正方形DEFG的面积为多少?
如图,四边形DEFG是△ABC的内接正方形,AB=BC=6cm,∠B=45°,则正方形DEFG的面积为多少?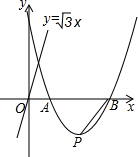 如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-4$\sqrt{3}$x+6$\sqrt{3}$与x轴交于A、B,点P为顶点,在直线y=$\sqrt{3}$x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标,若不存在,请说明理由.
如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-4$\sqrt{3}$x+6$\sqrt{3}$与x轴交于A、B,点P为顶点,在直线y=$\sqrt{3}$x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标,若不存在,请说明理由.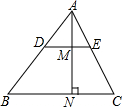 如图,△ABC,DE∥BC交AB、AC于D、E,AN⊥BC交DE于M点,若AD:DB=2:3,AM=3,则AN=$\frac{15}{2}$.若BC=8,则S△ADE=$\frac{24}{5}$.
如图,△ABC,DE∥BC交AB、AC于D、E,AN⊥BC交DE于M点,若AD:DB=2:3,AM=3,则AN=$\frac{15}{2}$.若BC=8,则S△ADE=$\frac{24}{5}$.