题目内容
10.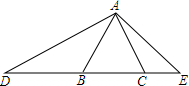 如图,在△ABC中,AB=AC,D、E为直线BC上的两点,且满足AB2=DB•CE,若∠BAC=50°,则∠DAE的度数为115°.
如图,在△ABC中,AB=AC,D、E为直线BC上的两点,且满足AB2=DB•CE,若∠BAC=50°,则∠DAE的度数为115°.
分析 根据AB=AC,求得∠ABD=∠ACE,再利用AB2=DB•CE证明△ADB∽△EAC,得出∠BAD=∠E,∠D=∠CAE,则∠DAE=∠BAD+∠BAC+∠CAE=∠D+∠BAD+∠BAC,很容易得出答案.
解答 证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=DB•CE
∴$\frac{AB}{CE}=\frac{DB}{AB}$,
∴$\frac{AB}{CE}=\frac{DB}{AC}$,
∴△ADB∽△EAC.
∴∠BAD=∠E,∠D=∠CAE,
∵∠DAE=∠BAD+∠BAC+∠CAE,
∴∠DAE=∠D+∠BAD+∠BAC,
∵∠BAC=40°,AB=AC,
∴∠ABC=65°,
∴∠D+∠BAD=65°,
∴∠DAE=∠D+∠BAD+∠BAC=65°+50°=115°
故答案为115°.
点评 本题主要考查了相似三角形的判定,等腰三角形的性质,以及学生对相似三角形的判定这一知识点的理解和掌握,难度不大,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5. 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )| A. | $\widehat{AC}$ | B. | $\widehat{AD}$ | C. | $\widehat{ACD}$ | D. | $\widehat{ADB}$ |
15.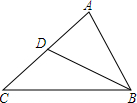 如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )
如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )
 如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )
如图,在△ABC中,点D是AC边上的一点,且AB是AD与AC的比例中项,则下列结论中,错误的是( )| A. | ∠C=∠ABD | B. | ∠ABC=∠ADB | C. | $\frac{BD}{BC}$=$\frac{AD}{AC}$ | D. | $\frac{BD}{BC}$=$\frac{AD}{AB}$ |
 如图,反比例函数y=$\frac{k}{x}$的图象经过点(5,4),若y>4,则x的取值范围是0<x<5.
如图,反比例函数y=$\frac{k}{x}$的图象经过点(5,4),若y>4,则x的取值范围是0<x<5.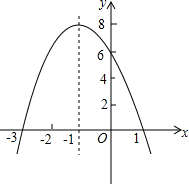 已知y=ax2+bx+c(a≠0)的图象,根据图象回答下列问题.
已知y=ax2+bx+c(a≠0)的图象,根据图象回答下列问题.
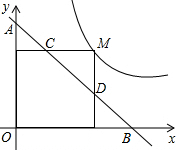 如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-$\sqrt{3}$x+m于点D、C两点,若直线y=-$\sqrt{3}$x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为4.
如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-$\sqrt{3}$x+m于点D、C两点,若直线y=-$\sqrt{3}$x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为4. 已知:如图,∠1=∠C,∠2=∠D,求证:∠3=∠4.
已知:如图,∠1=∠C,∠2=∠D,求证:∠3=∠4.