��Ŀ����
6���Ķ�����㣺�Ķ����²��ϣ��������Ӧ������쳲�������Լ1170-1250�����������ѧ�ң����о���һ������ �������dz��������Ϊ쳲��������У�����һ��˳�������ŵ�һ �������dz��������Ϊ쳲��������У�����һ��˳�������ŵ�һ������Ϊ���У��������������о����Ĺ����У��������������벻�� �Ľ������ʵ�������У��ܶ�䣨��÷��������ݡ����پյȣ��� ����ǡ��쳲����������е�����쳲��������л��кܶ���Ȥ�����ʣ� ��ʵ��������Ҳ�й㷺��Ӧ�ã� 쳲����������еĵ�n����������$\frac{1}{\sqrt{5}}[��\frac{1+\sqrt{5}}{2}��^{n}-��\frac{1-\sqrt{5}}{2}��^{n}]$ ��ʾ������n��1������������������ʾ��������һ�������� |
���� ��n=1��n=2�ֱ����ʽ�ӻ�����ô𰸼��ɣ�
��� �⣺��1��������n=1ʱ��
$\frac{1}{\sqrt{5}}$��$\frac{1+\sqrt{5}}{2}$-$\frac{1-\sqrt{5}}{2}$��=$\frac{1}{\sqrt{5}}$��$\sqrt{5}$=1��
��2��������n=2ʱ��
$\frac{1}{\sqrt{5}}$[��$\frac{1+\sqrt{5}}{2}$��2-��$\frac{1-\sqrt{5}}{2}$��2]
=$\frac{1}{\sqrt{5}}$��$\frac{1+\sqrt{5}}{2}$+$\frac{1-\sqrt{5}}{2}$����$\frac{1+\sqrt{5}}{2}$-$\frac{1-\sqrt{5}}{2}$��
=$\frac{1}{\sqrt{5}}$��1��$\sqrt{5}$
=1��
���� ���⿼����θ�ʽ�Ļ�����㡢������ֵ�Լ�Ӧ�ã��������⣬�ҳ�����ķ����ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
16��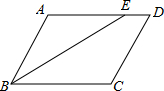 ��ͼ����?ABCD�У�BEƽ�֡�ABC��AD��E��BC=8cm��CD=6cm����D=60�㣬������˵���д�����ǣ�������
��ͼ����?ABCD�У�BEƽ�֡�ABC��AD��E��BC=8cm��CD=6cm����D=60�㣬������˵���д�����ǣ�������
 ��ͼ����?ABCD�У�BEƽ�֡�ABC��AD��E��BC=8cm��CD=6cm����D=60�㣬������˵���д�����ǣ�������
��ͼ����?ABCD�У�BEƽ�֡�ABC��AD��E��BC=8cm��CD=6cm����D=60�㣬������˵���д�����ǣ�������| A�� | ��C=120�� | B�� | AE=6cm | C�� | AD=8cm | D�� | ��BED=140�� |
 ��ͼ��ABΪ�ġ�0�ң���D��C�ڡ�0�ϣ�����AD=BC����֤����ABD�ա�BAC��
��ͼ��ABΪ�ġ�0�ң���D��C�ڡ�0�ϣ�����AD=BC����֤����ABD�ա�BAC��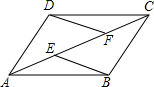 ��֪����ͼ��E��F��?ABCD�ĶԽ���AC�����㣬AF=CE����֤��DF=BE��DF��BE��
��֪����ͼ��E��F��?ABCD�ĶԽ���AC�����㣬AF=CE����֤��DF=BE��DF��BE��