题目内容
1.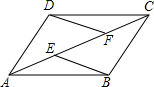 已知:如图,E,F是?ABCD的对角线AC上两点,AF=CE,求证:DF=BE,DF∥BE.
已知:如图,E,F是?ABCD的对角线AC上两点,AF=CE,求证:DF=BE,DF∥BE.
分析 可由题中条件求解△ABE≌△CDF,得出DF=BE,∠AEB=∠CFD,即∠BEC=∠DFA,进而可求证DF与BE平行.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
又∵AE=CF,
∴△ABE≌△CDF(SAS),
∴DF=BE,∠AEB=∠CFD,
∴∠BEC=∠DFA,
∴DF∥BE.
点评 本题主要考查了平行四边形的性质及全等三角形的判定及性质,能够运用其性质解决一些简单的证明问题,解题的关键是能够证得△ABE≌△CDF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.阅读与计算:阅读以下材料,并完成相应的任务.
任务:请根据以上材料,通过计算求出裴波那契数列中的第1个数和第2个数.
斐波那契(约1170-1250)是意大利数学家,他研究了一列数, 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到 的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的 瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质, 在实际生活中也有广泛的应用. 斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$ 表示(其中n≥1),这是用无理数表示有理数的一个范例. |
11.分别顺次连接①平行四边形;②矩形;③菱形;④对角线相等的四边形“各边中点所构成的四边形”中,为菱形的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
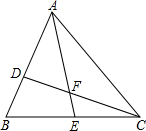 如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.
如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4. 如图,AB∥CD,点E在CD上,且BA=BE,∠AEC=70°,那么∠B=40°.
如图,AB∥CD,点E在CD上,且BA=BE,∠AEC=70°,那么∠B=40°.