题目内容
15．计算：（1）（-$\sqrt{3}$）0÷（-2）-2-23×2-2
（2）（2x-1）（2x+1）-（x-6）（4x+3）
分析 （1）原式利用零指数幂、负整数指数幂法则，以及乘方的意义计算即可得到结果；
（2）原式利用平方差公式，以及多项式乘以多项式法则计算即可得到结果．
解答 解：（1）原式=1×4-8×$\frac{1}{4}$=4-2=2；
（2）原式=4x2-1-（4x2+3x-24x-18）=4x2-1-4x2+21x+18=21x+17．
点评 此题考查了实数的运算，以及整式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
6．阅读与计算：阅读以下材料，并完成相应的任务．
任务：请根据以上材料，通过计算求出裴波那契数列中的第1个数和第2个数．
斐波那契（约1170-1250）是意大利数学家，他研究了一列数， 这列数非常奇妙，被称为斐波那契数列（按照一定顺序排列着的一列数称为数列）．后来人们在研究它的过程中，发现了许多意想不到 的结果，在实际生活中，很多花朵（如梅花、飞燕草、万寿菊等）的 瓣数恰是斐波那契数列中的数，斐波那契数列还有很多有趣的性质， 在实际生活中也有广泛的应用． 斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}[（\frac{1+\sqrt{5}}{2}）^{n}-（\frac{1-\sqrt{5}}{2}）^{n}]$ 表示（其中n≥1），这是用无理数表示有理数的一个范例． |
如图，AB∥CD，点E在CD上，且BA=BE，∠AEC=70°，那么∠B=40°．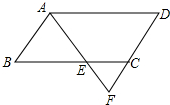
如图，在平行四边形ABCD中，E是BC上一点，且AB=BE，AE的延长线交DC的延长线于点F，若∠F=62°，则∠D=56度．
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是⊙O外一点，PA切⊙O于点A，且PA=PB．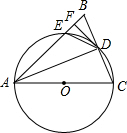
如图，在△ABC中，AB=AC，以AB为直径作⊙O，分别交BC、AC于点D、E，连接AD，过点D作DF⊥AB，垂足为点F．