题目内容
3. 已知,如图,在△ABC中,DE垂直平分BC,∠BAC的平分线交DE于点O,OM⊥AB于M,ON⊥AC的延长线于N.求证:BM=CN.
已知,如图,在△ABC中,DE垂直平分BC,∠BAC的平分线交DE于点O,OM⊥AB于M,ON⊥AC的延长线于N.求证:BM=CN.
分析 因为ED是BC的垂直平分线,那么BD=CD,而AD是∠BAC的平分线,DM⊥AB,DN⊥AC,根据角平分线的性质可得DM=DN,再根据HL可判定Rt△BMD≌Rt△CND,从而有BM=CN.
解答 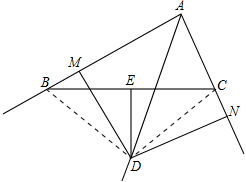 证明:连接BD,CD,如图,
证明:连接BD,CD,如图,
∴DE是BC的垂直平分线,
∴BD=CD,
∵AD是∠BAC的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△BMD和Rt△CND中,
$\left\{\begin{array}{l}{BD=CD}\\{DM=DN}\end{array}\right.$,
∴Rt△BMD≌Rt△CND(HL),
∴BM=CN.
点评 本题考查了全等三角形的判定和性质、线段垂直平分线的性质,解题的关键是掌握垂直平分线的定义以及性质,掌握角平分线的性质以及具体的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
8.某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教,每人只能去一个镇,则恰好其中一镇去4名,另两镇各去1名的概率为( )
| A. | $\frac{20}{81}$ | B. | $\frac{10}{81}$ | C. | $\frac{5}{243}$ | D. | $\frac{10}{243}$ |

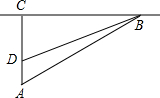 校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.
校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.