题目内容
18.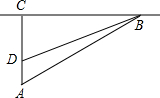 校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.
校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.(1)求CD的长.(结果保留根号)
(2)问这辆车在本路段是否超速?请说明理由(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.73)
分析 (1)作DE∥AB交BC于E,则∠CDE=∠A,设CD=x米,求出∠CED=30°,得出DE=2CD=2x,CE=$\sqrt{3}$x,证明BE=DE=2x,由BC=$\sqrt{3}$AC得出方程,解方程即可;
(2)由(1)得:x=20$\sqrt{3}$,得出BC的长,求出校车从B到C匀速行驶的速度,即可得出结论.
解答 解:(1)作DE∥AB交BC于E,如图所示: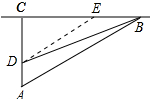 则∠CDE=∠A=60°,
则∠CDE=∠A=60°,
设CD=x米,
∵AC⊥l,
∴∠ACB=90°,
∴∠CED=30°,
∴DE=2CD=2x,
∴CE=$\sqrt{3}$x,
∵∠BDC=75°,
∴∠BDE=15°,
∵∠CED=∠BDE+∠DBE,
∴∠DBE=15°=∠BDE,
∴BE=DE=2x,
又∵∠A=60°,
∴BC=$\sqrt{3}$AC,
∴$\sqrt{3}$x+2x=$\sqrt{3}$(x+40),
解得:x=20$\sqrt{3}$,
即CD=20$\sqrt{3}$米;
(2)这辆车在本路段不超速;理由如下:
由(1)得:x=20$\sqrt{3}$,
∴BC=CE+BE=$\sqrt{3}$×20$\sqrt{3}$+2×20$\sqrt{3}$=60+40$\sqrt{3}$(米),
校车从B到C匀速行驶用时10秒,
速度为(60+40$\sqrt{3}$)÷10=6+4$\sqrt{3}$(米/秒)≈46.67千米/小时<50千米/小时,
∴这辆车在本路段不超速.
点评 本题考查了勾股定理的运用、平行线的性质、三角函数的运用;熟练掌握勾股定理的运用,通过作辅助线求出CD是解决问题的关键.

练习册系列答案
相关题目
9. 在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
青年人日均发微信条数统计表
请你根据以上信息解答下列问题:
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某市常住人口中20~35岁的青年人大约有30万人,试估计其中“日均发微信条数”不少于20条的大约有多少万人.
 在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):
在某项针对20~35岁的青年人每天发微信数量的调查中,设一个人的“日均发微信条数”为m,规定:当0≤m<10时为A级,10≤m<20时为B级,20≤m<30时为C级,30≤m<40时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微信条数”的调查,根据调查数据整理并制作图表如图(青年人日均发微信条数直方图):青年人日均发微信条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<10) | 90 | 0.3 |
| B级(10≤m<20) | 120 | a |
| C级(20≤m<30) | b | 0.2 |
| D级(30≤m<40) | 30 | 0.1 |
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某市常住人口中20~35岁的青年人大约有30万人,试估计其中“日均发微信条数”不少于20条的大约有多少万人.
6.在某中学举行的演讲比赛中,七年级5名参赛选手的成绩及平均成绩如下表所示:
那么根据表中提供的数据,计算这5名选手比赛成绩的方差是6.8.
| 选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 平均成绩 |
| 得分 | 90 | 95 | 93 | 89 | 88 | 91 |
13.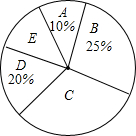 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
(1)本次被调查的学生数为120人;
(2)统计表中a的值为42;
(3)扇形统计图中C组所在扇形圆心角为126度;
(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时的学生人数.
 近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.| 组别 | A | B | C | D | E |
| 锻炼时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
| 人数 | 12 | 30 | a | 24 | 12 |
(2)统计表中a的值为42;
(3)扇形统计图中C组所在扇形圆心角为126度;
(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时的学生人数.
 已知,如图,在△ABC中,DE垂直平分BC,∠BAC的平分线交DE于点O,OM⊥AB于M,ON⊥AC的延长线于N.求证:BM=CN.
已知,如图,在△ABC中,DE垂直平分BC,∠BAC的平分线交DE于点O,OM⊥AB于M,ON⊥AC的延长线于N.求证:BM=CN.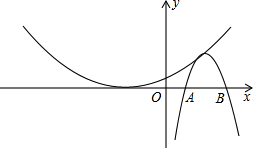 定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.
定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.