题目内容
8.某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教,每人只能去一个镇,则恰好其中一镇去4名,另两镇各去1名的概率为( )| A. | $\frac{20}{81}$ | B. | $\frac{10}{81}$ | C. | $\frac{5}{243}$ | D. | $\frac{10}{243}$ |
分析 因为对于这六个人来说,会被随机分派到3个镇中的任何一个,所以一共有36种情况,而有4个人的镇可能是3个镇中的任何一个,剩下两个镇各派一个人的派法是3×C64,根据概率公式求解.
解答 解:6名教师志愿随机派到3个镇中的任何一个共有36种情况,有4个人的镇可能是3个镇中的任何一个,另两镇各去1名的结果数为3×6×5,
所以恰好其中一镇去4名,另两镇各去1名的概率=$\frac{3×6×5}{{3}^{6}}$=$\frac{10}{81}$.
故选B.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | (a2)4=a8 | C. | a3•a2=a6 | D. | (a-b)2=a2-b2 |
18.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.
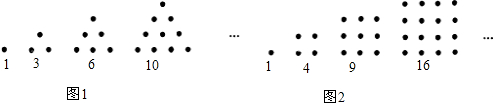
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
(1)按照规律,表格中a=28,b=36,c=35.
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
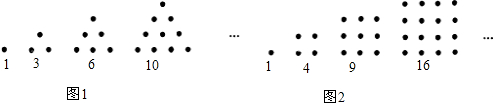
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
| 三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
| 正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
| 五边形数 | 1 | 5 | 12 | 22 | C | 51 | 70 | … |
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
 已知,如图,在△ABC中,DE垂直平分BC,∠BAC的平分线交DE于点O,OM⊥AB于M,ON⊥AC的延长线于N.求证:BM=CN.
已知,如图,在△ABC中,DE垂直平分BC,∠BAC的平分线交DE于点O,OM⊥AB于M,ON⊥AC的延长线于N.求证:BM=CN.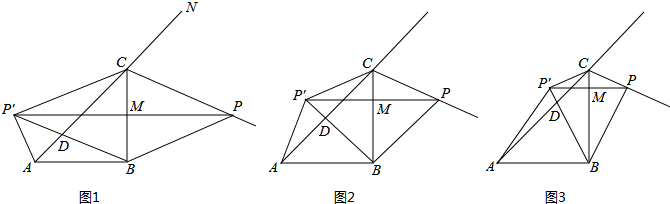
 定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.
定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.