题目内容
3.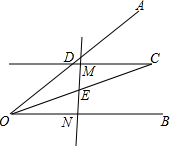 如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.
如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.
分析 (1)当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.首先根据OC是∠AOB的平分线,CD∥OB,判断出∠DOC=∠DC0,所以OD=CD=DM+CM;然后根据E是线段OC的中点,CD∥OB,推得CM=ON,即可判断出OD=DM+ON,据此解答即可.
(2)当点M在线段CD延长线上时,线段OD、ON、DM之间的数量关系是:OD=ON-DM.由(1),可得OD=DC=CM-DM,再根据CM=ON,推得OD=ON-DM即可.
解答 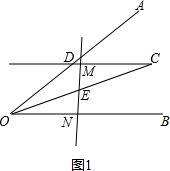 解:(1)当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.
解:(1)当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.
证明:如图1,
∵OC是∠AOB的平分线,
∴∠DOC=∠C0B,
又∵CD∥OB,
∴∠DCO=∠C0B,
∴∠DOC=∠DC0,
∴OD=CD=DM+CM,
∵E是线段OC的中点,
∴CE=OE,
∵CD∥OB,
∴$\frac{CM}{ON}$=$\frac{CE}{OE}$=1,
∴CM=ON,
又∵OD=DM+CM,
∴OD=DM+ON.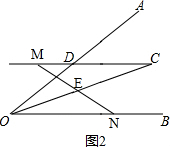
(2)当点M在线段CD延长线上时,线段OD、ON、DM之间的数量关系是:OD=ON-DM.
证明:如图2,
由(1),可得
OD=DC=CM-DM,
又∵CM=ON,
∴OD=DC=CM-DM=ON-DM,
即OD=ON-DM.
点评 (1)此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.②定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
(2)此题还考查了等腰三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.


(1)根据上面多面体的模型及表格中的数据:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
(2)一个多面体每个顶点处都有3条棱,多面体的棱数比顶点数大10,则这个多面体的面数是12;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.
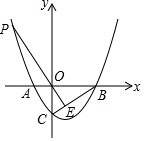 如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E.
如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E. 实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.
实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.
 如图,△ABC中,∠AED=∠B,AD=2,DB=4,AE=3,则EC=1.
如图,△ABC中,∠AED=∠B,AD=2,DB=4,AE=3,则EC=1.