题目内容
15.如图,在△ABC与△A′B′C′中,∠ABC=∠A′B′C′,∠C=∠C′,BG和B′G′分别是这两个三角形的角平分线,AM,A′M′分别是BC,B′C′边上的中线,AN,A′N′分别是BC,B′C′边上的高,若AN:A′N′=5:3,AM=10,B′G′=5,求A′M′,BG的长.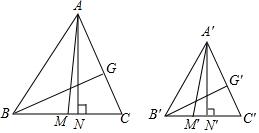
分析 证明△ABC∽△A′B′C′,由相似三角形的性质得出$\frac{AB}{A′B′}$=$\frac{AM}{A′M′}=\frac{BG}{B′G′}=\frac{AN}{A′N′}$=$\frac{5}{3}$,即可得出A′M′,BG的长.
解答 解:∵∠ABC=∠A′B′C′,∠C=∠C′,
∴△ABC∽△A′B′C′,
∴$\frac{AB}{A′B′}$=$\frac{AM}{A′M′}=\frac{BG}{B′G′}=\frac{AN}{A′N′}$=$\frac{5}{3}$,
∴$\frac{10}{A′M′}=\frac{BG}{5}=\frac{5}{3}$,
解得:A'M'=6,BG=$\frac{25}{3}$.
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定方法,熟记相似三角形的性质是解决问题的关键.

练习册系列答案
相关题目
6.在表中,我们把第i行第j列的数记为ai,j(其中i,j都是不大于4的正整数),对于表中的每个数ai,j,规定如下:当i>j时,ai,j=0;当i≤j时,ai,j=1.
例如:当i=4,j=1时,ai,j=a4,1=0.
(1)按此规定a1,3=1;
(2)请从下面两个问题中任选一个作答.
例如:当i=4,j=1时,ai,j=a4,1=0.
| a1,1 | a1,2 | a1,3 | a1,4 |
| a2,1 | a2,2 | a2,3 | a2,4 |
| a3,1 | a3,2 | a3,3 | a3,4 |
| a4,1 | a4,2 | a4,3 | a4,4 |
(2)请从下面两个问题中任选一个作答.
| 问题1 | 问题2 |
| a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0或3; | 表中的16个数中,共有10个1. |
10.下列说法正确的是( )
| A. | 三角形的外切圆有且只有一个 | |
| B. | 三角形的外心到这个三角形的三边距离相等 | |
| C. | 相等的圆心角所对的弧相等 | |
| D. | 等弧所对的圆心角相等 |
5.九年级某班部分同学利用课外活动时间,积极参加篮球定点投篮的训练,训练后的测试成绩如下表所示:
回答下列问题:
(1)训练后篮球定点投篮进球数的众数是4个,中位数是5个;
(2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数.
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定点投篮进球数的众数是4个,中位数是5个;
(2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数.
 如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=$\frac{1}{2}$,cot∠ABC=$\frac{3}{4}$,AD=8.
如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=$\frac{1}{2}$,cot∠ABC=$\frac{3}{4}$,AD=8.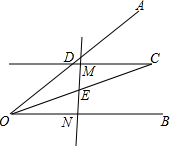 如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.
如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论. 如图,在等腰直角△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰直角△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.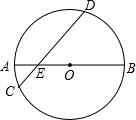 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长.