题目内容
11．在△ABC中，a2+b2=25，ab=12，且c=5，则最大边上的高是2.4．分析 根据勾股定理的逆定理，可得三角形为直角三角形，再根据三角形面积公式可求最大边上的高．
解答 解：∵a2+b2=25，c2=52=25，
∴a2+b2=c2，
∴三角形为直角三角形，
c为斜边，c上的高为h，由面积公式S=$\frac{1}{2}$ab=$\frac{1}{2}$ch，
∴h=$\frac{12}{5}$=2.4．
故答案为：2.4．
点评 本题考查了直角三角形的判定和三角形的面积公式的应用，勾股定理的灵活掌握及三角形的面积公式是解答的关键．
练习册系列答案
相关题目
如图，已知∠1=70°，∠2=110°，那么AB与CD平行吗？为什么？
如图，已知△ABC为等边三角形，点D在边AC上，点E在边AB上，且AD=BE，点F为线段DE的中点，求证：EC=2AF．
6．在表中，我们把第i行第j列的数记为ai，j（其中i，j都是不大于4的正整数），对于表中的每个数ai，j，规定如下：当i＞j时，ai，j=0；当i≤j时，ai，j=1．
例如：当i=4，j=1时，ai，j=a4，1=0．
（1）按此规定a1，3=1；
（2）请从下面两个问题中任选一个作答．
例如：当i=4，j=1时，ai，j=a4，1=0．
| a1，1 | a1，2 | a1，3 | a1，4 |
| a2，1 | a2，2 | a2，3 | a2，4 |
| a3，1 | a3，2 | a3，3 | a3，4 |
| a4，1 | a4，2 | a4，3 | a4，4 |
（2）请从下面两个问题中任选一个作答．
| 问题1 | 问题2 |
| a2，1•ai，j+a2，2•ai，j+a2，3•ai，j+a2，4•ai，j=0或3； | 表中的16个数中，共有10个1． |
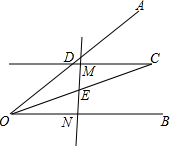如图，∠AOB平分线上一点C作CD∥OB交OA于点D，E是线段OC的中点，请过点E画直线分别交射线CD，OB于点M，N，探究线段OD，ON，DM之间的数量关系，并证明你的结论．
如图，在等腰直角△ABC中，∠A=90°，AB=AC，点D是斜边BC的中点，点E、F分别为AB、AC边上的点，且DE⊥DF．
如图，△ABC是等腰三角形，∠BAC=90°，D为BC延长线上一点，连续AD，以AD为边在AD右侧作正方形ADEF，连续FC、EC，若AC=$\sqrt{2}$，AD=$\sqrt{10}$．