题目内容
19.(1)用适当的方法解方程3x2+1=4x;(2)已知x1和x2是方程x2-3x-1=0的两个解,则x12x2+x1x22的值为.
分析 (1)将原方程变形为一般式,再利用分解因式法解方程即可;
(2)根据根与系数的关系可得出x1+x2=3、x1x2=-1,将其代入x12x2+x1x22=x1x2(x1+x2)中即可得出结论.
解答 解:(1)原方程可变形为3x2-4x+1=(3x-1)(x-1)=0,
解得:x1=$\frac{1}{3}$,x2=1.
(2)∵x1和x2是方程x2-3x-1=0的两个解,
∴x1+x2=3,x1x2=-1,
∴x12x2+x1x22=x1x2(x1+x2)=-3.
点评 本题考查了因式分解法解一元二次方程以及根与系数的关系,解题的关键是:(1)熟练掌握因式分解法解一元二次方程的方法;(2)根据根与系数的关系找出x1+x2=3、x1x2=-1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
 如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.很多运动员为了参加北京-张家口冬季奥运会,进行了积极的训练.下表记录了国家队4名队员在500米短道速滑训练成绩的平均数$\overline{x}$与方差s2:
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
| 队员甲 | 队员乙 | 队员丙 | 队员丁 | |
| 平均数$\overline{x}$(秒) | 45 | 46 | 45 | 46 |
| 方差s2(秒2) | 1.5 | 1.5 | 3.5 | 4.5 |
| A. | 队员甲 | B. | 队员乙 | C. | 队员丙 | D. | 队员丁 |
 如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.
如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.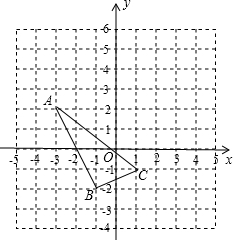 如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,得到△A1B1C1,完成下列问题:
如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,得到△A1B1C1,完成下列问题: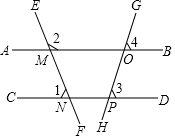 如图,已知∠1=68°,∠3=∠4,求∠2的度数.
如图,已知∠1=68°,∠3=∠4,求∠2的度数.