题目内容
14. 如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)根据角平分线的性质可得出DE=DF,结论(1)正确;
(2)由DE=DF、∠BED=∠GFD、BD=GD可证出△BDE≌△GDF(SAS),根据全等三角形的性质可得出∠B=∠DGF,结论(2)正确;
(3)利用全等三角形的判定定理AAS可证出△ADE≌△ADF,由此可得出AE=AF,根据△BDE≌△GDF可得出BE=GF,结合AB=AE+EB即可得出AB=AF+FG,结论(3)不正确;
(4)根据全等三角形的性质可得出S△ADE=S△ADF、S△BDE=S△GDF,结合S△ABD=S△ADE+S△BDE=50、S△ADG=S△ADF-S△GDF=38可求出△DFG的面积是6,结论(4)不正确.综上即可得出结论.
解答 解:(1)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,结论(1)正确;
(2)在△BDE和△GDF中,$\left\{\begin{array}{l}{DE=DF}\\{∠BED=∠GFD=90°}\\{BD=GD}\end{array}\right.$,
∴△BDE≌△GDF(SAS),
∴∠B=∠DGF,结论(2)正确;
(3)在△ADE和△ADF中,$\left\{\begin{array}{l}{∠EAD=∠FAD}\\{∠AED=∠AFD=90°}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△ADF(AAS),
∴AE=AF.
∵△BDE≌△GDF,
∴BE=GF,
∴AB=AE+EB=AF+FG,结论(3)不正确;
(4)∵△ADE≌△ADF,△BDE≌△GDF,
∴S△ADE=S△ADF,S△BDE=S△GDF.
∵S△ABD=S△ADE+S△BDE=50,S△ADG=S△ADF-S△GDF=38,
∴S△GDF=$\frac{50-38}{2}$=6,结论(4)不正确.
综上所述:正确的结论有(1)(2).
故选B.
点评 本题考查了全等三角形的判定与性质以及角平分线的性质,根据全等三角形的判定与性质和角平分线的性质逐一分析四条结论的正误是解题的关键.

 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案| A. | X | B. | L | C. | C | D. | Z |
 如图,平行四边形ABCD中,AC⊥AB,点E为BC边中点,AD=6,则AE的长为( )
如图,平行四边形ABCD中,AC⊥AB,点E为BC边中点,AD=6,则AE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
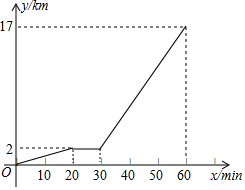 星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:
星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题: 已知:如图,四边形ABCD是菱形.以点D为圆心画弧,该弧分别与边AD、CD相交于点E、F,连接BE、BF.求证:BE=BF.
已知:如图,四边形ABCD是菱形.以点D为圆心画弧,该弧分别与边AD、CD相交于点E、F,连接BE、BF.求证:BE=BF.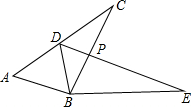 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.