题目内容
8.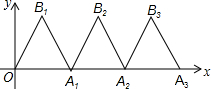 如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )| A. | 0 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 先判断△OB1A1为等边三角形,再根据平移得出,点A5的横坐标为20,点A6的横坐标为24,最后根据点P(23,n)在f6上,求得点P离x轴的距离即可.
解答 解:∵OB1=A1B1.∠OB1A1=60°,
∴△OB1A1为等边三角形,
由平移规律得,在f6中,点A5的横坐标为20,点A6的横坐标为24,
∴点B6的横坐标为22,
又∵点P(23,n)在f6上,
∴点P为线段A6B6的中点,
∴A6P=$\frac{1}{2}$A6B6=$\frac{1}{2}$×4=2,
又∵∠PA6A5=60°,
∴点P离x轴的距离为:2×sin60°=$\sqrt{3}$,
即n的值是$\sqrt{3}$.
故选(B).
点评 本题主要考查了坐标与图形变化,解决问题的关键是判断点P在f6中的具体位置.注意把一个图形整体沿某一直线方向移动,所得的新图形与原图形的形状和大小完全相同.

练习册系列答案
相关题目
20.下列分解因式正确的是( )
| A. | x2-x-3=x(x-1)-3 | B. | -xy2+2xy-y=-y(xy-2x) | ||
| C. | 2x2-xy=2x(x-y) | D. | 2x2-8x+8=2(x-2)2 |
13.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三内角之比为1:2:3 | B. | 三边长分别为5,12,14 | ||
| C. | 三边长之比为3:4:5 | D. | 三边长分别为1,$\sqrt{2}$,$\sqrt{3}$ |
17.下列运算中,结果正确的是( )
| A. | $\sqrt{36}$=±6 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{\frac{3}{4}}=\frac{{\sqrt{3}}}{2}$ |
18.下列命题是假命题的是( )
| A. | 两组对边分别相等的四边形是平行四边形 | |
| B. | 对角线相等的平行四边形是矩形 | |
| C. | 对角线垂直的平行四边形是菱形 | |
| D. | 四条边相等的四边形是正方形 |


 如图,平面直角坐标系的原点为点O,把直线y=-2x向上平移b(b>0)个单位,与x轴交于点A,与y轴交于点B,以下不同的三点D(x1,y1)、E(x2,y2)、F(x3,y3)的横纵坐标都是整数,且这三个点都在△AOB的内部(包括三角形边上).
如图,平面直角坐标系的原点为点O,把直线y=-2x向上平移b(b>0)个单位,与x轴交于点A,与y轴交于点B,以下不同的三点D(x1,y1)、E(x2,y2)、F(x3,y3)的横纵坐标都是整数,且这三个点都在△AOB的内部(包括三角形边上).