题目内容
20.如图,△ABC是等边三角形,AD所在直线是它的对称轴,把此三角形沿AD剪开,得到两个三角形,固定一个△ADC,现以D为旋转中心,把△ABD旋转n度,得到△A′B′D,如图2.(1)若n=40,则∠ADA′=40度;
(2)如图1,设A′D交AC于E,请用含n的式子表示∠DEC的度数;
(3)如图3,当n为何值时,A′B′∥DC,请说明理由.

分析 (1)根据旋转的性质即可得到结论;
(2)根据等边三角形的性质得到∠DAC=$\frac{1}{2}$∠BAC=30°,由三角形外角的性质的外角的性质即可得到结论.
(3)根据等边三角形的性质得到AD⊥BC,求得∠ADC=90°,得到∠A′DC=30°,推出∠A′=∠A′DC,根据平行线的判定定理即可得到结论.
解答 解:(1)∵把△ABD旋转n度,得到△A′B′D,
∴∠BDB′=∠ADA′=n°,
∵n=40,
∴∠ADA′=40°,
故答案为:40;
(2)∵△ABC是等边三角形,AD所在直线是它的对称轴,
∴∠DAC=$\frac{1}{2}$∠BAC=30°,
∴∠DEC=∠DAC+∠ADA′=30°+n°;
(3)当n=60时,A′B′∥DC,
∵△ABC是等边三角形,AD所在直线是它的对称轴,
∴AD⊥BC,
∴∠ADC=90°,
∵∠ADA′=60°,
∴∠A′DC=30°,
∵∠A′=∠DAC=30°,
∴∠A′=∠A′DC,
∴A′B′∥DC.
点评 本题考查了旋转的性质,等边三角形的性质,平行线的判定,熟练掌握旋转的性质是解题的关键.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 点P(1,-3)在笫二象限 | B. | 已知点A(-3,4),点B(-3,2),则AB∥x轴 | ||
| C. | 点M(3,-2)到y轴的距离为2个单位 | D. | 已知点A(1,2),点B(-2.-1),则AB=3$\sqrt{2}$ |
8.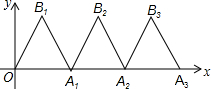 如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
 如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )| A. | 0 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
15.某顾客第一次在商店买若干个小商品花去5元;第二次再去买该小商品时,发现每一件(12个)降价0.8元,他第二次购买该小商品的数量是第一次的2倍,第二次共花去2元,该顾客第一次买的小商品是( )个.
| A. | 5 | B. | 20 | C. | 40 | D. | 60 |
12.下列说法中,正确的是( )
| A. | -(-3)2=9 | B. | |-3|=-3 | C. | $\sqrt{9}$=±3 | D. | $\root{3}{-64}$=-$\root{3}{64}$ |
9.一次函数y=3x-2的图象不经过第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
10.不等式1-2x<5-x的负整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 已知线段DE是由线段AB平移得到的,且AB=DC=4cm,EC=3cm,则△DCE的周长为11厘米.
已知线段DE是由线段AB平移得到的,且AB=DC=4cm,EC=3cm,则△DCE的周长为11厘米.