题目内容
17.下列运算中,结果正确的是( )| A. | $\sqrt{36}$=±6 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{\frac{3}{4}}=\frac{{\sqrt{3}}}{2}$ |
分析 根据二次根式的性质、加法、乘法、除法法则逐一计算后即可判断.
解答 解:A、$\sqrt{36}$=6,此选项错误;
B、3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,此选项错误;
C、$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$,此选项错误;
D、$\sqrt{\frac{3}{4}}$=$\frac{\sqrt{3}}{\sqrt{4}}$=$\frac{\sqrt{3}}{2}$,此选项正确;
故选:D.
点评 本题主要考查二次根式的混合运算,在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 如图,把△ABC绕点C顺时针旋转35°后,得到△A′B′C,A′B′交AC于点D,若∠A′=55°,∠B=50°,则∠ACB′的度数是( )
如图,把△ABC绕点C顺时针旋转35°后,得到△A′B′C,A′B′交AC于点D,若∠A′=55°,∠B=50°,则∠ACB′的度数是( )
 如图,把△ABC绕点C顺时针旋转35°后,得到△A′B′C,A′B′交AC于点D,若∠A′=55°,∠B=50°,则∠ACB′的度数是( )
如图,把△ABC绕点C顺时针旋转35°后,得到△A′B′C,A′B′交AC于点D,若∠A′=55°,∠B=50°,则∠ACB′的度数是( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
8.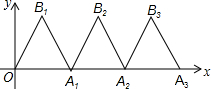 如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
 如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )| A. | 0 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
12.下列说法中,正确的是( )
| A. | -(-3)2=9 | B. | |-3|=-3 | C. | $\sqrt{9}$=±3 | D. | $\root{3}{-64}$=-$\root{3}{64}$ |
2.下列根式中,最简二次根式是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{8}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{\frac{1}{3}}$ |
9.一次函数y=3x-2的图象不经过第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
7.下列说法正确的是( )
| A. | 分数都是有理数 | B. | -a是负数 | ||
| C. | 有理数不是正数就是负数 | D. | 绝对值等于本身的数是正数 |
