题目内容
5.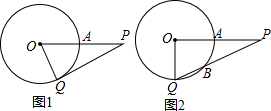 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
分析 (1)先利用切线的性质得到OQ⊥PQ,然后利用锐角三角函数值的定义求∠QOP的大小;
(2)利用垂径定理,作OD⊥BQ于D,如图2,则QD=BD,先利用勾股定理计算出PQ,再证明Rt△QOD∽Rt△QPO,利用相似比计算出QD,从而得到BQ的长.
解答 解:(1)如图1,∵PQ是⊙O的切线,
∴OQ⊥PQ,
∵A是OP的中点,
∴OP=2OA,
在Rt△OPQ中,cos∠QOP=$\frac{OQ}{OP}$=$\frac{1}{2}$,
∴∠QOP=60°;
(2)作OD⊥BQ于D,如图2,则QD=BD,
∵∠QOP=90°,OP=4,OQ=2,
∴PQ=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵∠OQD=∠PQO,
∴Rt△QOD∽Rt△QPO,
∴QD:OQ=OQ:QP,即QD:2=2:2$\sqrt{5}$,
∴QD=$\frac{2\sqrt{5}}{5}$,
∴QB=2QD=$\frac{4\sqrt{5}}{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.解决本题的关键是垂径定理和相似三角形的性质的运用.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
10.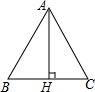 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
 如图,在平面直角坐标系中,△AOB是等边三角形,且边长为2,则点A的坐标为A(1,$\sqrt{3}$).
如图,在平面直角坐标系中,△AOB是等边三角形,且边长为2,则点A的坐标为A(1,$\sqrt{3}$). 如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.
如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.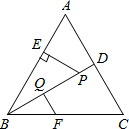 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长.
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长. 如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则:
如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则: