题目内容
16. 如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.
如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.
分析 根据解直角三角形找出部分A点的坐标,根据A点的坐标找出点的变化规律“A4n+1(3×$(\frac{2\sqrt{3}}{3})^{4n}$,0),A4n+2(0,3×$(\frac{2\sqrt{3}}{3})^{4n+1}$),A4n+3(-3×$(\frac{2\sqrt{3}}{3})^{4n+2}$,0),A4n+4(0,-3×$(\frac{2\sqrt{3}}{3})^{4n+3}$)”,由此规律即可找出点A2015的横坐标.
解答 解:∵Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…中,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°,
∴OA1=3,OA2=$\frac{O{A}_{1}}{cos∠{A}_{2}O{C}_{2}}$=2$\sqrt{3}$,OA3=$\frac{O{A}_{2}}{cos∠{A}_{3}O{C}_{3}}$=4,OA4=$\frac{O{A}_{3}}{cos∠{A}_{4}O{C}_{4}}$=$\frac{8\sqrt{3}}{3}$,OA5=$\frac{O{A}_{4}}{cos∠{A}_{5}O{C}_{5}}$=$\frac{16}{3}$,…,
∴A1(3,0),A2(0,2$\sqrt{3}$),A3(-4,0),A4(0,-$\frac{8\sqrt{3}}{3}$),A5($\frac{16}{3}$,0),…,
∴发现规律:A4n+1(3×$(\frac{2\sqrt{3}}{3})^{4n}$,0),A4n+2(0,3×$(\frac{2\sqrt{3}}{3})^{4n+1}$),A4n+3(-3×$(\frac{2\sqrt{3}}{3})^{4n+2}$,0),A4n+4(0,-3×$(\frac{2\sqrt{3}}{3})^{4n+3}$).
∵2015=503×4+3,
∴点A2015的横坐标为-3×$(\frac{2\sqrt{3}}{3})^{2014}$=-4×$(\frac{4}{3})^{1006}$.
点评 本题考查了规律型中的点的坐标,解题的关键是找出点的变化规律“A4n+1(3×$(\frac{2\sqrt{3}}{3})^{4n}$,0),A4n+2(0,3×$(\frac{2\sqrt{3}}{3})^{4n+1}$),A4n+3(-3×$(\frac{2\sqrt{3}}{3})^{4n+2}$,0),A4n+4(0,-3×$(\frac{2\sqrt{3}}{3})^{4n+3}$)”.本题属于中档题,难度不大,解决该题型题目时,根据解直角三角形找出部分点A的坐标,根据点A的坐标找出点的变化规律是关键.

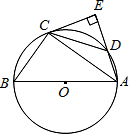 如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.(1)求证:DC=BC;
(2)若AB=10,AC=8,求tan∠DCE的值.
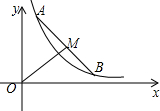 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$-1 |
| A. |  | B. |  | C. |  | D. |  |
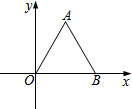 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )| A. | (2,$\sqrt{3}$) | B. | (2,4) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,2) |
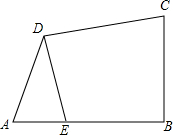 已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.
已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.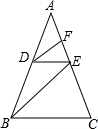 已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.
已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.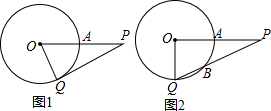 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.