题目内容
17.(1)计算:$\sqrt{32}$-3$\sqrt{\frac{1}{2}}$+$\sqrt{2}$(2)解不等式,并将解集在数轴上表示出来:$\frac{x-1}{2}$-$\frac{x+4}{3}$>-2.
分析 (1)根据二次根式的乘除法,可化简二次根式,根据合并同类项二次根式,可得答案;
(2)根据解不等式的步骤,可得答案.
解答 解:(1)原式=4$\sqrt{2}$-$\frac{3}{2}$$\sqrt{2}$+$\sqrt{2}$=$\frac{7\sqrt{2}}{2}$;
(2)去分母,得3(x-1)-2(x+4)>-12,
去括号,得3x-3-2x-8>-12
移项,得3x-2x>-12+3+8
合并同类项,得x>-1.
点评 本题考查了二次根式的加减,先化简二次根式,再合并同类二次根式.

练习册系列答案
相关题目
6.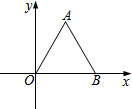 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )| A. | (2,$\sqrt{3}$) | B. | (2,4) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,2) |
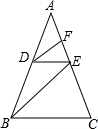 已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.
已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.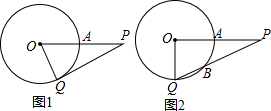 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.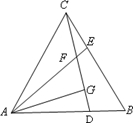 如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.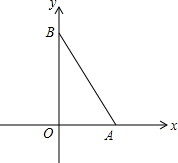 已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标.
已知点A的坐标为(2,0),点B的坐标为(0,4),作等边△ABC,求点C的坐标.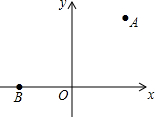 如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).
如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).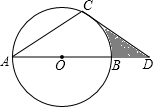 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.