题目内容
20. 如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则:
如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则:(1)点D的坐标为($\frac{1}{3}$,3);
(2)设P是反比例函数图象上的动点,则线段PB长度的最小值是$\sqrt{7}$.
分析 (1)设点B的坐标为(m,m)(m>0),根据比例关系找出点D的坐标,将点D的坐标代入到反比例函数中即可得出关于m的一元二次方程,解方程即可得出m的值,将其代入点D的坐标中即可得出结论;
(2)设点P的坐标为(n,$\frac{1}{n}$)(n>0),由点B的坐标利用两点间的距离公式找出BP=$\sqrt{(n+\frac{1}{n}-3)^{2}+7}$,根据二次函数的性质即可找出BP的最小值.
解答 解:(1)设点B的坐标为(m,m)(m>0),
∵AD:DB=1:8,
∴AD:AB=1:9,
即点D的坐标为($\frac{m}{9}$,m).
将点D的坐标代入y=$\frac{1}{x}$中,得m=$\frac{1}{\frac{m}{9}}$,
即m2=9,解得:m=±3.
∴点D的坐标为($\frac{1}{3}$,3).
故答案为:($\frac{1}{3}$,3).
(2)设点P的坐标为(n,$\frac{1}{n}$)(n>0),
∵点B的坐标为(3,3),
∴BP=$\sqrt{(3-n)^{2}+(3-\frac{1}{n})^{2}}$,
=$\sqrt{{n}^{2}-6n+9+\frac{1}{{n}^{2}}-\frac{6}{n}+9}$,
=$\sqrt{(n+\frac{1}{n})^{2}-6(n+\frac{1}{n})+9+7}$,
=$\sqrt{(n+\frac{1}{n}-3)^{2}+7}$,
当n+$\frac{1}{n}$-3=0时,BP取最小值$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查了反比例函数图象上点的坐标特征以及两点间的距离公式,解题的关键是:(1)用m表示出点D的坐标;(2)找出线段BP=$\sqrt{(n+\frac{1}{n}-3)^{2}+7}$.本题属于基础题,难度不大,解决该题型题目时,利用两点间的距离公式表示出线段BP的长度是解题的关键.

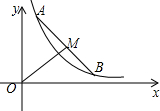 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$-1 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 34.383×1011 | B. | 3.4383×1012 | C. | 3.4383×1013 | D. | 3.4383×1011 |
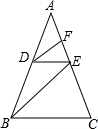 已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.
已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.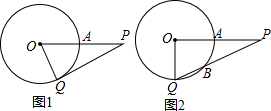 已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
已知:P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.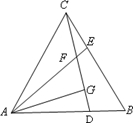 如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.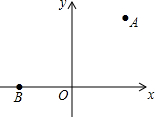 如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).
如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).