题目内容
2．
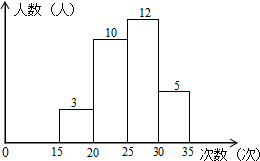某学校为了解七年级学生的体能情况，随机选取30名学生测试一分钟仰卧起坐次数，并绘制了如图的直方图，学生仰卧起坐次数在20～25之间的频率为$\frac{1}{3}$．
分析 根据直方图得出一分钟仰卧起坐次数在20～25之间的频数，然后依据频率=频数÷数据总数求解即可．
解答 解：10÷30=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 本题主要考查的是频数分布直方图的应用，找出一分钟仰卧起坐次数在20～25之间的频数是解题的关键．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
12．若∠A是锐角，且cosA=sinA，则∠A的度数是（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 不能确定 |
13．下列从左到右的变形，是因式分解的是（ ）
| A． | （3-x）（3+x）=9-x2 | B． | （y+1）（y-3）=（3-y）（y+1） | ||
| C． | 4yz-2y2z+z=2y（2z-zy）+z | D． | -8x2+8x-2=-2（2x-1）2 |
10．已知函数y=$\frac{1}{x-3}$，自变量x的取值范围是（ ）
| A． | x≠3且x≠0 | B． | x＞3 | C． | x＜3 | D． | x≠3 |
河堤的横断面如图1，堤高10米，迎水斜坡AB长26米，那么斜坡AB的坡度i是1：2.4．
7．已知一次函数y=kx+b的图象经过点（-2，-6），（0，4），则当y=0时，x的值为（ ）
| A． | $-\frac{2}{5}$ | B． | $-\frac{4}{5}$ | C． | $\frac{4}{5}$ | D． | $\frac{2}{5}$ |
14．
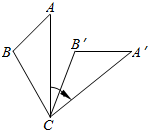如图，将△ABC绕着点C顺时针旋转50°后得到△A′B′C′，若∠A=45°，∠B′=110°，则∠BCA′的度数是（ ）
如图，将△ABC绕着点C顺时针旋转50°后得到△A′B′C′，若∠A=45°，∠B′=110°，则∠BCA′的度数是（ ）| A． | 55° | B． | 75° | C． | 95° | D． | 110° |
11．下列二元一次方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$的是（ ）
| A． | $\left\{\begin{array}{l}{x-y=1}\\{3x+y=5}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-2y=-3}\\{3x+y=5}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x-y=-1}\\{3x+y=-5}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-y=3}\\{3x-y=1}\end{array}\right.$ |
