题目内容
12.如图,正方形ABCD的对角线交于点O,正方形OEFG的顶点F在BC的延长线上,OE交BC于点H,连接OF.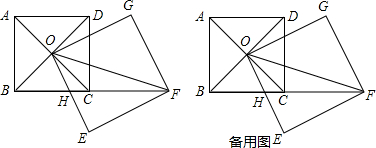
(1)求证:OH2=HC•HF;
(2)设HC=x,BF=y,若OB=5,请求出y与x的函数表达式.
分析 (1)根据正方形的性质得到∠BCO=∠EOF=45°,根据相似三角形的性质即可得到结论;
(2)根据正方形的性质得到∠OCB=∠OBC=45°,OB=OC=5,根据相似三角形的性质得到$\frac{HC}{OB}=\frac{OC}{BF}$,把HC=x,BF=y,OB=OC=5代入 即可得到结论.
解答 (1)证明:∵四边形ABCD与四边形OEFG是正方形,
∴∠BCO=∠EOF=45°,
又∵∠CHO=∠OHF,
∴△CHO∽△OHF,
∴$\frac{OH}{HF}=\frac{CH}{OH}$,
∴OH2=HC•HF;
(2)解:∵四边形ABCD是正方形,
∴∠OCB=∠OBC=45°,OB=OC=5,
由(1)知∠EOF=45°,
∴∠OBC=∠EOF,
∵∠OHC=∠OBC+∠BOH,∠BOF=∠EOF+∠BOH,
∴∠OHC=∠BOF,
∵∠OCB=∠OBC,
∴△OHC∽△FOB,
∴$\frac{HC}{OB}=\frac{OC}{BF}$,
∵HC=x,BF=y,OB=OC=5,
∴$\frac{x}{5}=\frac{5}{y}$,
∴y=$\frac{25}{x}$.
点评 本题考查了正方形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
20.下列命题中,是真命题的是( )
| A. | 若a>b,则|a|>|b| | B. | 若|a|>|b|,则a>b | C. | 若a=b,则a2=b2 | D. | 若a2=b2,则a=b |
7.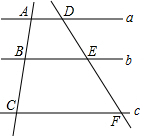 如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
 如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | $\frac{10}{3}$ | D. | $\frac{15}{2}$ |
1.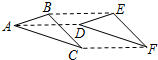 如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
 如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )| A. | BC∥EF | B. | AD=BE | C. | BE∥CF | D. | AC=EF |
2.下列几组数中,能作为直角三角形三边长度的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 6,8,11 | D. | 5,12,13 |
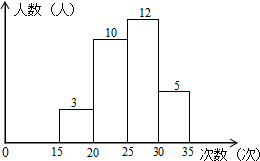 某学校为了解七年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在20~25之间的频率为$\frac{1}{3}$.
某学校为了解七年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在20~25之间的频率为$\frac{1}{3}$. 已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.