题目内容
17. 河堤的横断面如图1,堤高10米,迎水斜坡AB长26米,那么斜坡AB的坡度i是1:2.4.
河堤的横断面如图1,堤高10米,迎水斜坡AB长26米,那么斜坡AB的坡度i是1:2.4.
分析 根据勾股定理求出BC的长,根据坡度的概念计算即可.
解答 解:由勾股定理得,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=24米,
则斜坡AB的坡度i=AC:BC=1:2.4,
故答案为:1:2.4.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列条件中,不能判定四边形ABCD是平行四边形的是( )
| A. | ∠A=∠C,∠B=∠D | B. | AB∥CD,AB=CD | C. | AB∥CD,AD∥BC | D. | AB=CD,AD∥BC |
9.下列语句中,是假命题的是( )
| A. | 所有的实数都可用数轴上的点表示 | B. | 等角的补角相等 | ||
| C. | 互补的两个角是邻补角 | D. | 垂线段最短 |
6. 已知四边形ABCD是平行四边形,下列结论不正确的是( )
已知四边形ABCD是平行四边形,下列结论不正确的是( )
 已知四边形ABCD是平行四边形,下列结论不正确的是( )
已知四边形ABCD是平行四边形,下列结论不正确的是( )| A. | 当AB=BC时,它是菱形 | B. | 当∠ABC=90°时,它是矩形 | ||
| C. | 当AC⊥BD时,它是菱形 | D. | 当AC=BD时,它是正方形 |
7.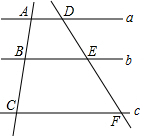 如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
 如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | $\frac{10}{3}$ | D. | $\frac{15}{2}$ |
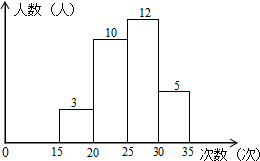 某学校为了解七年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在20~25之间的频率为$\frac{1}{3}$.
某学校为了解七年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在20~25之间的频率为$\frac{1}{3}$.