题目内容
14.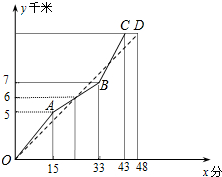 如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.
如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.
分析 已经求出第一次相遇的时间;求出直线BC的解析式,联立直线OD的解析式即可得出第二次相遇的时间.
解答 解:根据甲15-33分钟运动了2千米,
所以可得甲这段时间的速度为:$\frac{1}{9}$km/分,
故从5千米运动至6千米需要9分钟,
即6千米对应的时间为24分钟,
可得:第一次相遇的时间是第24分钟;
点B的坐标为(33,7),点C的坐标为(43,12),
设直线BC的解析式为y=ax+b,则$\left\{\begin{array}{l}{33a+b=7\\;}\\{43a+b=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{19}{2}}\end{array}\right.$,
即直线BC的解析式为y=$\frac{1}{2}$x-$\frac{19}{2}$,
联立直线OD与直线BC的解析式可得:$\left\{\begin{array}{l}{y=\frac{1}{4}x}\\{y=\frac{1}{2}x-\frac{19}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=38}\\{y=\frac{19}{2}}\end{array}\right.$,
即第二次相遇的时间是第38分钟,
所以乙领先甲时的x的取值范围是24<x<38.
故答案为:24<x<38.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决;得到甲乙两人在不同阶段内的速度是解决本题的易错点.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
5.若不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x+a>0}\end{array}\right.$的解集为2<x≤3,则a,b的值分别为( )
| A. | -2,3 | B. | 2,-3 | C. | 3,-2 | D. | -3,2 |
19.函数$y=(m+1){x}^{{m}^{2}+m-1}$是反比例函数,则m的值为( )
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 0或1 |
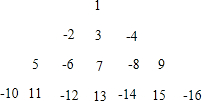 将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.
将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.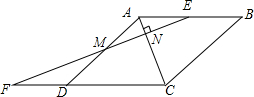 如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.
如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.