题目内容
3.若关于x的方程$\frac{x+2}{x-2}+\frac{x-2}{x+2}+\frac{4x+a}{{{x^2}-4}}=0$只有一个实数根,则符合条件的所有实数a的值的总和为( )| A. | -6 | B. | -30 | C. | -32 | D. | -38 |
分析 分式方程去分母转化为整式方程,分类讨论整式方程只有一个实数根,检验后求出a的值总和即可.
解答 解:已知方程化为2x2+4x+a+8=0①,
若方程①有两个相等实根,则△=16-8(a+8)=0,即a=-6,
当a=-6时,方程①的根x1=x2=-1,符合要求;
若x=2是方程①的根,则8+8+a+8=0,即a=-24,
此时,方程①的另一个根为x=-4,符合要求;
若x=-2是方程①的根,则8-8+a+8=0,即a=-8,
此时方程①的另一个根为x=0,符合要求,
综上,符合条件的a有-6,-24,-8,其总和为-38,
故选D
点评 此题考查了分式方程的解,利用了分类讨论的思想,注意分式方程有解,即最简公分母不能为0.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
12.下列函数是二次函数的是( )
| A. | y=3x+1 | B. | y=ax2+bx+c | C. | y=x2+3 | D. | y=(x-1)2-x2 |
13.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示.
请你根据表中数据选一人参加比赛,最合适的人选是丁.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
| 方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.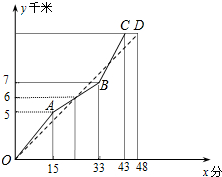 如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.
如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.