题目内容
若n为任意整数，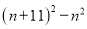 
的值总可以被k整除，则k等于（ ）
A. 11 B. 22 C. 11或22 D. 11的倍数
A
【解析】(n+11)2-n2=(n+11+n)(n+11-n)=11(11+2n)，所以可以被11整除，
故选A.
练习册系列答案
相关题目
为了了解参加某运动会的2000名运动员的年龄情况，从中抽查了100名运动员的年龄，“某运动员被抽到”这一事件是______事件．
随机.
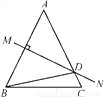
【解析】由题意知是从2000名运动员的年龄中抽取100名运动员的年龄，每一名运动员被投到的频率为，即为，所以某运动员被抽到这一事件是随机事件. 如图，等腰△ABC中，AB＝AC，∠DBC＝15°，AB的垂直平分线MN交AC于点D，则∠A的度数是________．
50°
【解析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD，根据等边对等角可得∠A=∠ABD，然后表示出∠ABC，再根据等腰三角形两底角相等可得∠C=∠ABC，然后根据三角形的内角和定理列出方程求解即可．
【解析】
∵MN是AB的垂直平分线，
∴AD=BD，
∴∠A=∠ABD，
∵∠DBC=15°，
∴∠ABC=∠A+15°，
∵AB=AC... 关于中心对称的两个图形的关系是___________
全等
【解析】关于中心对称的两个图形是全等图形.
故答案：全等. 已知下列命题：（ ）
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
其中真命题的个数是
A. 1个 B. 2个 C. 3个 D. 0个
A
【解析】关于中心对称的两个图形一定是全等图形，但是两个全等图形不一定关于中心对称；故选A. 利用因式分解简便计算（要求写出完整计算过程）
(1) 
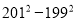（2）
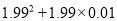
(1)800;(2)3.98.
【解析】试题分析：（1）利用平方差公式得到原式=（201+199）×（201-199），然后进行有理数运算；
（2）利用提公因式得到原式=1.99×（1.99+0.01），然后进行有理数运算．
试题解析：（1）原式=（201+199）×（201-199）
=400×2
=800；
（2）原式=1.99×（1.99+0.01）
... 分解因式：①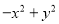
=____________ ；②
=_________________．
；
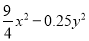【解析】①=y2-x2=（y+x）（y-x）；
②= (9x2-y2)= (3x+y)(3x-y)，
故答案为：①；② . 如图，A、B两点的坐标分别为(2,3)、(4,1)．
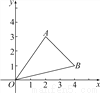
(1)求△ABO的面积；
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
（1）S△ABO＝5；（2）A′(2,0)，B′(4，－2)，O′(0，－3)．
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO＝3×4－×3×2－×4×1－×2×2＝5,
(2)A′(2,0),B′(4,－2),O′(0,－3)． 已知抛物线y＝ax2－2x＋1与x轴没有交点，那么该抛物线的顶点所在的象限是( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
D
【解析】∵抛物线y＝ax2－2x＋1与x轴没有交点，
∴△=4-4a＜0，
解得a＞1，
∴抛物线的开口向上，
又∵b=-2，
∴ ＞0，
∴抛物线的对称轴在y轴的右侧，
∴抛物线的顶点在第一象限.
故选D．