题目内容
为了了解参加某运动会的2000名运动员的年龄情况，从中抽查了100名运动员的年龄，“某运动员被抽到”这一事件是______事件．
随机.
【解析】由题意知是从2000名运动员的年龄中抽取100名运动员的年龄，每一名运动员被投到的频率为，即为，所以某运动员被抽到这一事件是随机事件.
练习册系列答案
步步高达标卷系列答案
相关题目
命题“全等三角形的面积相等”的逆命题是 ．
面积相等的两个三角形全等
【解析】试题分析：把一个命题的题设和结论互换就可得到它的逆命题： “全等三角形的面积相等”的逆命题是：面积相等的三角形是全等三角形． 如图所示、△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°，D在AB上．
（1）求证：△AOC≌△BOD；
（2）若AD=1，BD=2，求CD的长．
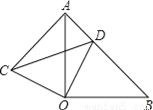
（1）证明见解析；（2）CD的长为．
【解析】（1）证明：如右图1，
，
又，
（2）由有： ， ，
，故 如图，平行四边形ABCD中，AC=4cm，BC=5cm，CD=3cm，则?ABCD的面积__．
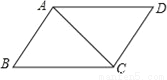
12cm2
【解析】 ∵四边形ABCD是平行四边形，
∴AB=CD=3cm，
∵AC=4cm，BC=5cm，
∴AC2+AB2=AC2，
∴△ABC是直角三角形，
∴S△ABC=×3×4=6cm2，
∴则ABCD的面积=2×6=12cm2. 掷一枚质地均匀的骰子，看落地后朝上的面的点数.
（1）会出现哪些可能的结果？
（2）掷出的点数为1与掷出的点数为2的频率相同吗？掷出的点数为1与掷出的点数为3的频率相同吗？
（3）每种结果出现的频率相同吗？
（1）可能出现朝上的面的点数是：1，2，3，4，5，6；（2）掷出的点数为1与掷出的点数为2的频率相同；掷出的点数为1与掷出的点数为3的频率相同；（3）每种结果出现的频率相同
【解析】试题分析: 掷一个质地均匀的骰子，有6种等可能的结果，每个数字的频率都稳定在 ，所以每种结果出现的可能性都相同.
（1）【解析】
掷一枚质地均匀的骰子，由于有六个面，所以落地后，可能出现朝上的面的点数是... 从一副扑克牌中则下列事件中可能性最大的是( )
A. 抽出一张红心 B. 抽出一张红色老K C. 抽出一张梅花J D. 抽出一张不是Q的牌
D
【解析】一副扑克牌有54张，其中红桃、黑桃、梅花、方块各13张，大、小王各一张，所以，任意抽出一张，抽到红桃的概率为，抽到黑桃的概率为，抽到梅花的概率为，抽到大、小王的概率为，抽出一张不是Q牌的概率为，对照这些数据，可以得到可能性最大的是D.
故选D. 下列事件发生的可能性为0的是（ ）
A. 掷两枚骰子，同时出现数字“6”朝上
B. 小明从家里到学校用了10分钟，从学校回到家里却用了15分钟
C. 今天是星期天，昨天必定是星期六
D. 小明步行的速度是每小时40千米
D
【解析】对于A，掷两枚骰子，同时出现数字“6”朝上，可能性为；
对于B，小明从家里到学校用了10分钟，从学校回到家里却用了15分钟是可能是，比如去学校时下坡，则回家时上坡，当然回家比去学校用时多；
对于C，今天是星期天，昨天必定是星期六这是一个必然发生的事件，可能性为1；
对于D，小明步行的速度是每小时40千米，是不存在的.一般人步行的速度为3－5公里每小时，所以D发生... 如图，在?ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则阴影部分的面积为( )
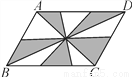
A. 3 B. 6 C. 12 D. 24
C
【解析】∵四边形ABCD为平行四边形，∴OA=OC，OB=OD，
∴△OBE≌△ODH，△OAQ≌△OCG，△OPD≌△OFB，∴S阴影=S△BCD，
∴S△BCD=S平行四边形ABCD=×6×4=12．故选C. 若n为任意整数，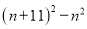 
的值总可以被k整除，则k等于（ ）
A. 11 B. 22 C. 11或22 D. 11的倍数
A
【解析】(n+11)2-n2=(n+11+n)(n+11-n)=11(11+2n)，所以可以被11整除，
故选A.