题目内容
已知抛物线y＝ax2－2x＋1与x轴没有交点，那么该抛物线的顶点所在的象限是( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
D
【解析】∵抛物线y＝ax2－2x＋1与x轴没有交点，
∴△=4-4a＜0，
解得a＞1，
∴抛物线的开口向上，
又∵b=-2，
∴ ＞0，
∴抛物线的对称轴在y轴的右侧，
∴抛物线的顶点在第一象限.
故选D．
练习册系列答案
相关题目
若n为任意整数，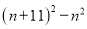 
的值总可以被k整除，则k等于（ ）
A. 11 B. 22 C. 11或22 D. 11的倍数
A
【解析】(n+11)2-n2=(n+11+n)(n+11-n)=11(11+2n)，所以可以被11整除，
故选A. 如图，A、B两点的坐标分别为(2,3)、(4,1)．
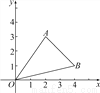
(1)求△ABO的面积；
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
（1）S△ABO＝5；（2）A′(2,0)，B′(4，－2)，O′(0，－3)．
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO＝3×4－×3×2－×4×1－×2×2＝5,
(2)A′(2,0),B′(4,－2),O′(0,－3)． 抛物线y=2x2+4x+m与x轴只有一个公共点，则m的值为____
2
【解析】∵抛物线与x轴只有一个公共点，
∴△=0，
∴b2-4ac=42-4×2×m=0；
∴m=2．
故答案为：2. 已知抛物线y=x2-x-1与x轴的交点为（m，0），则代数式m2-m+2011的值为（ ）
A. 2009 B. 2012 C. 2011 D. 2010
B
【解析】∵物线y=x2-x-1与x轴的交点为（m，0），
∴将x=m，y=0代入抛物线解析式得：m2-m-1=0，
∴m2-m=1，
则m2-m+2011=1+2011=2012．
故选：B. 如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
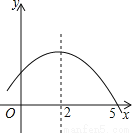
A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5
D
【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0），
∴函数图象与x轴的另一交点坐标为（-1，0），
∴ax2+bx+c＜0的解集是x＜-1或x＞5．
故选C. 简便计算：7.292﹣2.712=__．
45.8
【解析】7.292﹣2.712=(7.29+2.71)(7.29-2.71)=10×4.58=45.8. 在△ABC中，AB =AC，∠A=80°，则∠B=__________.
50°
【解析】∵AB=AC，
∴根据轴对称的性质，将线段BC对折重合后，点A在折痕上，
∴线段AB、AC关于折痕轴对称，
设折痕与BC交点为D，
则△ABD、△ACD关于直线AD轴对称，
∴∠B=∠C =(180°－∠A)÷2=（180°－80°)÷2=50°.
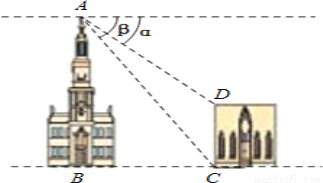
故答案为：50°. 如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为 m（结果不作近似计算）．
【解析】
试题分析：过点D作DE⊥AB于点E，
则四边形BCDE是矩形，
根据题意得：∠ACB=β=60°，∠ADE=α=30°，BC=18m，
∴DE=BC=18m，CD=BE，
在Rt△ABC中，AB=BC•tan∠ACB=18×tan60°=18（m），
在Rt△ADE中，AE=DE•tan∠ADE=18×tan30°=6（m），
∴DC=BE=AB...