题目内容
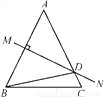
如图，等腰△ABC中，AB＝AC，∠DBC＝15°，AB的垂直平分线MN交AC于点D，则∠A的度数是________．
50°
【解析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD，根据等边对等角可得∠A=∠ABD，然后表示出∠ABC，再根据等腰三角形两底角相等可得∠C=∠ABC，然后根据三角形的内角和定理列出方程求解即可．
【解析】
∵MN是AB的垂直平分线，
∴AD=BD，
∴∠A=∠ABD，
∵∠DBC=15°，
∴∠ABC=∠A+15°，
∵AB=AC...
练习册系列答案
考前必练系列答案
相关题目
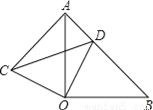
如图所示、△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°，D在AB上．
（1）求证：△AOC≌△BOD；
（2）若AD=1，BD=2，求CD的长．
（1）证明见解析；（2）CD的长为．
【解析】（1）证明：如右图1，
，
又，
（2）由有： ， ，
，故 下列事件发生的可能性为0的是（ ）
A. 掷两枚骰子，同时出现数字“6”朝上
B. 小明从家里到学校用了10分钟，从学校回到家里却用了15分钟
C. 今天是星期天，昨天必定是星期六
D. 小明步行的速度是每小时40千米
D
【解析】对于A，掷两枚骰子，同时出现数字“6”朝上，可能性为；
对于B，小明从家里到学校用了10分钟，从学校回到家里却用了15分钟是可能是，比如去学校时下坡，则回家时上坡，当然回家比去学校用时多；
对于C，今天是星期天，昨天必定是星期六这是一个必然发生的事件，可能性为1；
对于D，小明步行的速度是每小时40千米，是不存在的.一般人步行的速度为3－5公里每小时，所以D发生... 如图，在?ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则阴影部分的面积为( )
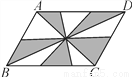
A. 3 B. 6 C. 12 D. 24
C
【解析】∵四边形ABCD为平行四边形，∴OA=OC，OB=OD，
∴△OBE≌△ODH，△OAQ≌△OCG，△OPD≌△OFB，∴S阴影=S△BCD，
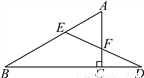
∴S△BCD=S平行四边形ABCD=×6×4=12．故选C. 如图，在△ABC中，∠ACB＝90°，D是BC延长线上一点，E是BD垂直平分线与AB的交点，DE交AC于点F.求证：点E在AF的垂直平分线上．
见解析
【解析】试题分析：过E作EG垂直于AC，交AC于G，可得出EG∥BD故∠AEG=∠B，∠D=∠DEG．再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D，根据ASA定理得出△AEG≌△FEG，进而可得出结论．
试题解析：
证明：如图所示：
过E作EG垂直于AC，交AC于G，
∵∠ACB=90°，
∴EG∥BD，
∴∠AEG=∠B，∠D=∠DEG．
∵... 全等的两个图形一定关于中心对称吗？
不一定
【解析】【试题分析】考查中心对称图形问题.
【试题解析】
全等的两个图形不一定是关于中心对称，因为还要找到对称中心.
故答案：不一定. 判断对错：两个会重合的图形一定是中心对称图形； ___________
错
【解析】两个会重合的图形不一定是中心对称图形，因为还要看是否存在对称中心.
故答案：错. 若n为任意整数，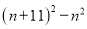 
的值总可以被k整除，则k等于（ ）
A. 11 B. 22 C. 11或22 D. 11的倍数
A
【解析】(n+11)2-n2=(n+11+n)(n+11-n)=11(11+2n)，所以可以被11整除，
故选A. 如图，A、B两点的坐标分别为(2,3)、(4,1)．
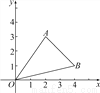
(1)求△ABO的面积；
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
（1）S△ABO＝5；（2）A′(2,0)，B′(4，－2)，O′(0，－3)．
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO＝3×4－×3×2－×4×1－×2×2＝5,
(2)A′(2,0),B′(4,－2),O′(0,－3)．